TAIL EFFICIENCY
Two aspects of the effect of elastic deformation of the horizontal tail and fuselage will be considered: the elastic efficiency of the horizontal tail and the static longitudinal stability of the airplane. The analysis will be made in an approximate manner. Only unswept wings and tails will be considered.
When an elevator angle changes, the pitching moment about the airplane center of gravity (c. g.) changes. If, originally, the airplane were in the condition of rectilinear symmetric steady flight, then the change of pitching moment induced by the elevator deflection would cause the airplane to pitch, and disturbed motion would ensue. In order to study the efficiency of the tail alone, however, it is more convenient to consider the unbalanced pitching moment, instead of the dynamics of the airplane as a whole. For this purpose, the airplane shall be assumed to be held fixed, against any disturbed motion, at the c. g. of the airplane. The wing and the structures in front of the c. g. shall not be disturbed. In this fictitious condition, the pitching moment (positive if it tends to increase the angle of attack) contributed by the horizontal tail surfaces, about the c. g., is
M = – lLt + Mt (1)
where Lt is the resultant lift of the tail, acting through the tail aerodynamic center; Mt is the pitching moment about the tail aerodynamic center; and l is the distance from the airplane c. g. to the resultant tail lift Lt. Generally, it is sufficiently accurate to assume Lt as normal to the fuselage reference axis, and to neglect the horizontal component of the aerodynamic forces. Then l is a constant independent of the angle of attack.
It is convenient to express the pitching moment about airplane c. g. by a moment coefficient based on wing area and wing chord; and L, and Mt by coefficients based on tail area and tail chord. Let ( )ш and ( )t denote quantities relating to wing and tail, respectively. Let q denote the dynamic pressure, S the area, c the chord length. We define
The bar over cw and ct indicates mean aerodynamic chords. qt denotes the dynamic pressure at the tail region, which, due to wing-fuselage interference and engine slip stream, may be slightly different from the free-stream dynamic pressure q.
A measure of the tail efficiency is the rate of change of the pitching – moment coefficient with elevator deflection, dCMjd/3, ft being the (symmetric) elevator deflection angle (positive if deflected downward). Owing to the elastic deformation of the tail and the fuselage, the derivative ЗС, И/Э/3 for a real airplane is smaller than that of a rigid airplane. The ratio
![]() ЗСм I /ЭСМ
ЗСм I /ЭСМ
эpiw ;rigid
+ /дч
Э/S qSw cw dp cw dp )
To compute the derivatives dCLtjdp, dCMt/dp, it is necessary to consider the elastic deformation of the airplane. The airplane structure can be represented by a skeleton system of beams as shown in Fig. 4.11. The tail angles of attack shall be represented by a characteristic number 0, measured at a reference section located at a spanwise coordinate rjt. If Wing
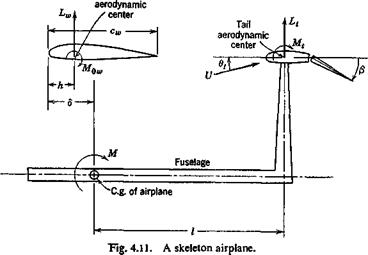 |
the tail angle-ofiattack distribution is described by 60f(y), у being the spanwise coordinate, then щ may be defined according to the following equation:
= % f(Vt) = sr f ЛУ) Ф) dy (5)
where st is the tail semispan, and St is the tail area. Hence 6t is a weighted average of the tail angle of attack. If a semirigid mode of the tail twisting f(y) is assumed, rt can be evaluated at once. Generally it lies at 2/3 to 3/4 semispan outboard from the fuselage.
The elastic property of the tail and fuselage may be described by two stiffness-influence coefficients Кг and K2 defined as follows. Let Kt be the total lift force (with KJ2 acting at each of the reference sections on the two halves of the horizontal tail) that is required to act at the tail aerodynamic center to produce a rotation of 1 radian at the tail reference
section,* with the fuselage assumed clamped at the airplane c. g. Let K2 be the total pitching moment (with KJ2 acting at each reference section) that is required to act at the tail reference sections to produce the same rotation. Then the total change of the tail angle of attack is
![]()
![]() (6)
(6)
To evaluate the derivatives involved in Eq. 4, it is only necessary to consider a small deflection angle Д/S. In the following, the quantities /8, 0t, Lt, and Mt will denote the changes corresponding to Д/S, and the symbol Д will be omitted. Let us assume that the strip assumption may be used and that the lift-curve slope at and the derivatives dCLt/cfS == аъ 8CMt/df3 з – m of the tail airfoil section be evaluated at the steady flight conditions. Then, if 6t is defined as in Eq. 5, we have Lt = qtSt(atOt + аф)
Mt = – m(SqtStct
|
where** |
Combining Eqs. 6 and 7, we obtain
|
From Eqs. 7 and 8, and according to the definitions 2, we derive
* Actually we are interested only in small deflections, so the linearity of the structural property can be assumed. **If the aerodynamic moment of the elevator is resisted by a control stick, the quantity m in A, Eq. 9 and Eq. 16 infra, should be replaced by 8Смі/8[} — SCm/Sf} where Chi is the hinge moment coefficient of the elevator based on the tail area and tail chord. Elsewhere no change is needed. |
The elastic efficiency of the elevator is therefore
|
І / |
‘pcy Э0 у |
1 , Al l / mcA-1 | – 1 + ГГв2 + – J-) rigid ■Ui"w * |
(13) |
|
(if et<l) E #2 |
(14) |
We may define, in analogy with the wing divergence, the critical divergence speed of the horizontal tail at which an infinitesimal change in /3 induces a large tail twist. According to Eq. 8 this occurs when В = 0,
i. e., when
![]()
![]() A
A
Stat
If K± is negative, then qt div given by Eq. 15 has no physical meaning, but is merely a parameter showing that the tail is stable.
|
*Ї_ _£*_ Stct atm |
We may also define a critical horizontal tail-control reversal speed at which a change of elevator angle produces no change in the pitching moment about the airplane c. g. This occurs when the tail efficiency becomes zero. Using the approximate formula 14, we obtain, at the reversal speed,
Note that qtiev is independent of Kb because at the reversal speed the tail lift due to elevator deflection vanishes. Using Eqs. 15 and 16, we may write
Elastic efficiency of elevator = ;——– -*(–■—v (17)
1 – qttit aw











