The Kutta condition

How can potential flow be adapted to provide a reasonable theoretical model for the flow around an aerofoil that generates lift? The answer lies in drawing an analogy between the flow around an aerofoil and that around a spinning cylinder (see Section 3.3.10). For the latter it can be shown that when a point vortex is superimposed with a doublet on a uniform flow, a lifting flow is generated. It was explained in Section 3.3.9 that the doublet and uniform flow alone constitutes a non-circulatory irrota – tional flow with zero vorticity everywhere. In contrast, when the vortex is present the vorticity is zero everywhere except at the origin. Thus, although the flow is still irrotational everywhere save at the origin, the net effect is that the circulation is non­zero. The generation of lift is always associated with circulation. In fact, it can be shown (see Eqn 3.52) that for the spinning cylinder the lift is directly proportional to the circulation. It will be shown below that this important result can also be extended to aerofoils. The other point to note from Fig. 3.25 is that as the vortex strength, and therefore circulation, rise both the fore and aft stagnation points move downwards along the surface of the cylinder.

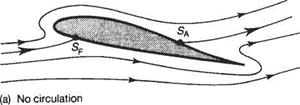
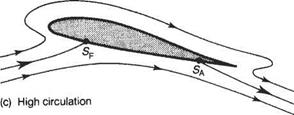
Now suppose that in some way it is possible to use vortices to generate circulation, and thereby lift, for the flow around an aerofoil. The result is shown schematically in Fig. 4.1. Figure 4.1a shows the pure non-circulatory potential flow around an aerofoil at an angle of incidence. If a small amount of circulation is added the fore and aft stagnation points, SF and SA, move as shown in Fig. 4.1b. In this case the rear stagnation point remains on the upper surface. On the other hand, if the circulation is relatively large the rear stagnation point moves to the lower surface, as shown in Fig. 4.1c. For all three of these cases the flow has to pass around the trailing edge. For an inviscid flow this implies that the flow speed becomes infinite at the trailing edge. This is evidently impossible in a real viscous fluid because viscous effects ensure that such flows cannot be sustained in nature. In fact, the only position for the rear stagnation point that is sustainable in a real flow is at the trailing edge, as illustrated in Fig. 4.Id. Only with the rear stagnation point at the trailing edge does

the flow leave the upper and lower surfaces smoothly at the trailing edge. This is the essence of the Kutta condition first introduced by the German mathematician Kutta.[11] Imposing the Kutta condition gives a unique way of choosing the circulation for an aerofoil, and thereby determining the lift. This is extremely important because otherwise there would be an infinite number of different lifting flows, each corres­ponding to a different value of circulation, just as in the case of the spinning cylinder

Fig. 4.2 for which the lift generated depends on the rate of spin. In summary, the Kutta condition can be expressed as follows.

• For a given aerofoil at a given angle of attack the value of the circulation must take the unique value which ensures that the flow leaves the trailing edge smoothly.

• For practical aerofoils with trailing edges that subtend a finite angle – see Fig. 4.2a – this condition implies that the rear stagnation point is located at the trailing edge.

All real aerofoils are like Fig. 4.2a, of course, but (as in Section 4.2) for theoretical reasons it is frequently desirable to consider infinitely thin aerofoils, Fig. 4.2b. In this case and for the more general case of a cusped trailing edge the trailing edge need not be a stagnation point for the flow to leave the trailing edge smoothly.

• If the angle subtended by the trailing edge is zero then the velocities leaving the upper and lower surfaces at the trailing edge are finite and equal in magnitude and direction.