Traveling Wave Solution

In the preceding section, a modal solution was obtained for the string problem. The solution depicted the total displacement as a summation of specific shapes as measured relative to the ends of the string. Each shape had an amplitude that was, in general, a function of time. When these individual modal contributions were of constant amplitude at their modal frequency, they appeared as standing or fixed waves along the string.

Another interpretation of the string response is now considered by examining the solution obtained for a string with an initial displacement but zero initial velocity and external loading. In this case, the Eis were all zero so that the displacement was written as

v(x,1) = Esin (i?) Ficos (Vm?) (3.56)

The Fis can be determined from the initial shape, f (x), as

Fi = 1 fo f (x) sin (dX (3.57)

It also may be noted that the initial shape can be represented by

СО у ч

v(x, 0) = f (x) = J2 Pi sin ( ^ ) (3.58)

i =1 ‘ ‘

Equation (3.58) is known as the Fourier sine series representation of the function f (x). Additional information on the Fourier series may be found in more advanced textbooks on structural dynamics and applied mathematics. Now, to rewrite the general solution for this problem, the two well-known identities

sin(a + в) = sin(a) cos(e) + cos(a) sin(e)

sin(a – в) = sin(a) cos(e) – cos(a) sin(e)

can be added to yield another identity as

1

sin(a) cos(e) = і [sin(a + в) + sin(a – в)]

This identity can be used to rewrite the general solution given by Eq. (3.56) as

Equation (3.58) gives the functional form of f (x) as an infinite sum of sine func­tions with coefficients Fi. The two terms on the right-hand side of Eq. (3.61) are of the same form as the sum in Eq. (3.58) and can be identified as having the func­tional form of f (x) but with different arguments. It is therefore possible to rewrite Eq. (3.61) as

This is the principal result of the traveling-wave solution. In reality, it is mathemati­cally identical to the previously given standing-wave solution in Eq. (3.56); the only difference is point of view.

To illustrate how Eq. (3.62) represents traveling waves along the string, the two arguments of the shape function are replaced by new spatial coordinates, the origins of which are time dependent. The new coordinates are defined as

Equation (3.62) becomes

1

v(x>t) = 2 [ f (xL) + f (xR)] (3.64)

which indicates that the time-dependent string shape is the sum of two shapes of a form identical to the initial shape but of one half its magnitude. Initially, at t = 0, the origins of the xL and xR coincide with the x origin as

xL(x, 0) = 0 at x = 0 xR(x, 0) = 0 at x = 0

At any later time t > 0, the origins of xL and xR can be located by

These results indicate that the xL coordinate system is moving to the left with a speed V T/m and the xR coordinate system is moving to the right with the same speed. These origin positions are indicated in Fig. 3.3. As a consequence of these moving origins, the shape f (xL)/2 appears to propagate to the left and the shape

f (xr)/2 appears to propagate to the right. Both of these shapes will move at a constant propagation speed of

so that Eq. (3.62) may be written in the form

1

v(x, t) = 2[ f (x + Vt) + f (x – Vt)] (3.68)

This is also called D’Alembert’s form of the equation.

When these shapes reach one of the walls, the deflection must go to zero to satisfy the boundary conditions. This condition at each wall causes the shapes to be reflected in the opposite direction. These reflections appear as inverted shapes propagating away from the walls, again with the speed V = V T/m. This reflected-wave behavior is inherent to the Fourier sine series representation of f (x) given in Eq. (3.58). Determination of the string displacement at times subsequent to t = 0 requires the evaluation of f (x ± Vt) in Eq. (3.62). Although the function f (x) is defined only for the range 0 < x < £, the arguments x + Vt and x – Vt significantly exceed this range. The Fourier sine series for f(x), Eq. (3.58), possesses two distinct mathematical properties that permit evaluation of the function throughout the extended range of the argument and demonstrate the reflected-wave behavior.

First Property of f (x). Because all terms in the Fourier sine series for f (x) are odd functions of x, f (x) must also be an odd function. This property can be described as

f (-x) = ~f (x) (3.69)

It is immediately seen that this is a description of the reflected-wave behavior at the x = 0 wall.

Second Property of f (x). Because all terms in the Fourier sine series for f(x) are periodic in x with a period of 2£, then f (x) also must be periodic in x with a period of 2£. This property can be described as

f (x) = f (x + 2n£) for n = 0, ±1, ±2,… (3.70)

This relationship, in conjunction with the previously noted “odd” functionality of f (x), describes the reflected-wave behavior at the x = £ wall.

Figure 3.4. Example initial shape of wave

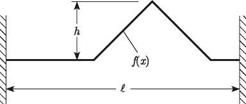General Evaluation of f (x ± Vt). These two properties can be applied simulta­neously for the evaluation of f (x + Vt) and f (x – Vt) for any value of their argument—say, x ± Vt. When this argument lies within the range

nt < x ± Vt < (n + 1)t (3.71)

where

n = 0, ±1, ±2,

then

We used Eq. (3.70) to reduce the range of motion, which wasinitially-to < x < +to, down to the range 0 < x < t, our physical space (i. e., where the string actually is mounted).

Example of Traveling Wave. The initial string shape is given in Fig. 3.4. At subse­quent times, the string shape appears as shown in Fig. 3.5. The absolute distance each of the half shapes has traveled at time t is denoted by x. The faint lines are the displacements associated with the two constituent waves after transformation to bring them into the range 0 < x < t, and the bold line is the sum of these two displacements. The displacement during the time t^/mfT < t < 2L/mfT is a mirror image of the progression revealed in Fig. 3.5 with a return to the original shape at t = 2tVm/ T. The motion is periodic thereafter with period 2L/mfT.