TWISTING OF PROPELLER BLADES

Divergence has an important bearing on many phases of the aeroelastic stability of propellers, not only because the steady-state instability in itself must be avoided, but also because of its close relationship to flutter. It was shown by Theodorsen and Regier4,36 that in some cases the blade simply twists to the stalling angle and initiates stall flutter when the speed is too close to the divergence speed. Thus the problem of pre­dicting propeller flutter is resolved primarily into the calculation of the speed at which the propeller will stall due to its aeroelastic twist, and the critical-divergence speed becomes a convenient criterion.

The divergence of propellers can be analyzed by the same methods as those exposed before, except that the effect of the centrifugal force must be added.

In a good propeller design, large bending stresses are avoided by making the normal component of the centrifugal force balance approximately the aerodynamic lift. Hence, it is a fair approximation to assume that the twisting moment acting on the blade consists in a couple formed by a lift force and a centrifugal-force component which is assumed equal to the lift.

Consider a representative se. ction of the propeller (Fig. 4.12). Let c be

the length of the chord, and xc be the distance from the center of mass to the leading edge. Then the twisting moment is

(Lift) • c(x — I)

This is balanced by the elastic moment. Let К be the torsional stiffness of the representative section defined as in Eq. 5 of § 3.3; then the equili­brium condition is

Кв = scx — )qa(xr + в — a0) (1)

where ar is the angle of attack of the section if the blade is perfectly rigid, в the angle of twist due to elasticity, oc0 the angle of attack for which there is no twist (to be explained later), q the dynamic pressure of the relative airstream, у a representative length of propeller blade, and a the lift-curve slope of the section.

The condition of divergence of the blade is that в -> со; i. e.,

в

*, + в — a0

The critical-divergence speed is then given by

К

Uv ~~ sc*a{x – 1)

From this equation, we see that the angle of twist increases rapidly when Ц f7div*

The conventional propeller design is based on the assumption of perfectly rigid blades. The design condition is stated in terms of ar or the corresponding lift coefficient CLr. The true lift coefficient CL of the elastic propeller is related to CLr by the relation

CL — CLr + ав (4)

The angle of attack for zero twist a0 can be calculated from the equi­librium of aerodynamic force and the centrifugal force. In the no-twist condition, the couple of the centrifugal force and the lift just balances the aerodynamic moment about the aerodynamic center, for which the moment coefficient is C:m. Hence, the equilibrium condition is

Cjiro + acr. Q(x i) = 0 (5)

provided that the angles a0 and ar are measured from the zero-lift line. Combining Eqs. 3 and 5 with 4, we obtain

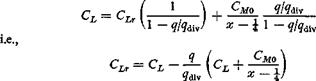(6)

(7)

The second term of the right-hand side of Eq. 7 is the increase in lift coefficient due to the elastic twist of the blade. This increase will be zero, and the blade will not be twisted, if the design lift coefficient is

This is the ideal design lift coefficient given by Theodorsen and Regier. For the Clark-Г airfoil with center of gravity at 44 per cent and CM0 = — 0.07, CLI is 0.37. In this case the angle of attack at zero elastic twist is not very far from the optimum angle of attack of the Clark – Y airfoil, which is at CL — 0.40. Since operating a blade at CLI delays the stall, and thus causes an increase in the flutter speed, it is desirable to operate the propeller at the ideal angle of attack.

In using Eq. 2 to determine the divergence speed, the choice of the radius of the representative sections is open to question. Usually the 80 per cent radius section is taken as the representative section, at which L, c, x, and the corresponding stiffness К are measured. A more rational basis is to use Lagrange’s equations or a method of successive approxima­

tion, similar to those of §§ 3.4, and 3.5. The arbitrariness of choosing a representative section can thus be avoided.

The closeness of the elastic axis, the inertia axis, and the line of aero­dynamic centers of practical propeller or helicopter blades makes such blades inherently strong against flutter. An exact flutter analysis, how­ever, must consider the nonuniform flow condition across the span, the centrifugal force, and the Coriolis force, and is not simple. See papers by Morris, Rosenberg, Duncan, Turner, etc., listed in the bibliography of Chapter 7.