Uniform Flow Plus Source-Sink Pair

As surmised from the preceding section, the superposition of a sink located down­stream of the source discussed yields the flow around a closed body—that is, pro­viding that the source and sink are of equal strength (i. e., net strength of zero indicating that the mass emanating from the source is absorbed by the sink). Thus, using Eqs. 4.30 and 4.31:

V = Vuf + V S1- V S2 = V~r sin 0 + 2П01-2n 02 , (440)

where 0 is the polar angle to the point in question and 01 and 02 are the angles between the positive x axis and straight lines joining the source-sink (respectively) and the point in question. By holding V and Л fixed and assigning different constant values to the stream function in Eq. 4.40, we can find different combinations of r, 0, 01,and 02 that satisfy this equation (i. e., 01 and 02 can be expressed in terms of r and 0 for a specified spacing between the source and sink). Then, the streamlines may be found by plotting curves, which are generated by varying the angle 0 and using Eq. 4.40 to solve for the radius r for a particular streamline corresponding to a constant value of v. Each value of v provides another streamline. The result of joining the dots is demonstrated in Program PSI.

RUNNING PROGRAM PSI 1. One streamline represents a closed body, as expected. Confirm that the body shape and size depends on the values of freestream velocity, source-sink strength, and source-sink spacing. 2. The body has two stagnation points, one at the front and the other at the rear. Their locations may be found by solving for u and v and setting both velocity components equal to zero. From this, the value of the stream function on this stagnation streamline follows. 3. The velocity singularities are located within the solid body. 4. The body shape looks like an ellipse but it is not; it is called a Rankine Ovoid.* 5. The student is encouraged to run Program PSI to obtain the streamline pat­terns when the source and sink strengths do not sum to zero.

Named after W. Rankine, a Scottish engineer who first solved this problem in the 1800s.

Uniform Flow Plus Doublet Flow Around a Cylinder

Q /2nVM 2 2 x[16] [17] + y2

The Cartesian-coordinate expression may be written as:

As before, we try to find the shape of the streamlines ¥ = constant. Here, the body shape may be found analytically. We ask the questions, “What is the shape of the streamline ¥ = 0?” From Eq. 4.42, the stream function is zero when:

y = 0; that is, along the x-axis or when

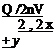
= 0 ^ x2 + y2 = -^= R2,

2nVM

which is a circle of radius R having a center at the origin.

Recall that when the stream function representing the freestream was deter­mined, the constant of integration was made zero by setting the stream function zero along the x-axis. Here, the x-axis is the streamline y = 0, but there is a singularity at x = 0, y = 0. That is, the stream function at the origin is indeterminate. Notice that this singularity presents no difficulty because the origin is inside the zero-streamline body. In particular, the zero-streamline body is a circle (i. e., a right circular cylinder in cross section) of radius R. The other streamlines outside the cylinder may be found by joining the dots as before, and the results are shown in Program PSI. Note that when running this program:

or the drag (i. e., streamwise) direction. The fact that there is no lift should not be surprising because there is no asymmetry in either of the superposed stream functions. In fact, introducing asymmetry is the next step. The result that there is no drag contradicts experience until it is realized that the flow model is inviscid, so that there are no boundary-layer effects present and, in particular, there is no large separated region (i. e., wake) behind the cylinder. In fact, as shown next, there are two stagnation points on the cylinder, both on the x-axis at +/- R. Clearly, this solution is of no value in describing the flow over the downstream side of a cylinder in a practical problem. However, the theory sat­isfactorily predicts the pressure distribution on the upstream side of a cylinder (or sphere), where the boundary layer is thin and remains attached. The solu­tion for a cylinder also is important in the development of inviscid-airfoil theory (see Chapter 5).

3. Note the distribution of static pressure around the cylinder. The pressure dis­tribution on the surface is symmetrical with respect to both the x and y axes; hence, there is no unbalanced force on the cylinder. The distribution-of-pressure coefficient is shown as well, which does not provide additional information but rather is intended to familiarize the student with such data presentations.

The polar-coordinate notation is reviewed in Fig. 4.14 to avoid confusion about signs. Note that the arrows on the velocity components indicate the positive direc­tion of the component and that the polar angle is measured from the positive x-axis, which here is the downstream direction.

1 Т/ a —-*- = V cos 0 r 00 ” -°^ = – V sin0 dr ”

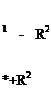The velocity components in polar coordinates are obtained by differentiating Eq. 4.41:

From this, it follows that on the surface of the cylinder (r = R), ur = 0. This is as it should be because there cannot be a flow component normal to a streamline. The fact that ur = 0 at the body surface r = R also indicates that the surface-boundary condition is satisfied. Also, from Eq. 4.43, u0 = -2V sin0 at r = R. Hence, there is a stagnation point on the body surface at 0 = n (i. e., the rear stagnation point on the

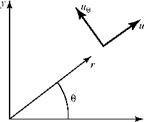Figure 4.14. Polar-coordinate notation.

x-axis) and at 0 = 0 (i. e., the front stagnation point on the x-axis). Upstream of the body along the x-axis, 0 = n and u0 = -2V sin0 = 0 and ur < V because R < r. By substituting different values for r, Program PSI shows how ur begins to decrease about 10 cylinder radius upstream of the stagnation point and then decreases to zero at an increasing rate as r approaches the cylinder radius. The velocity component u0 at the top of the cylinder (0 = n/2) exhibits similar behavior with r for r > R. Thus, the disturbance due to even this blunt body dies out rather quickly in this low-speed flow. Finally, Eq. 4.43 shows that far from the body, r ^ ^ and V = VTC, which satisfies the boundary condition.

At 0 = n/2 on the surface of the cylinder, the tangential velocity has the (maximum) value u0 = -2VM (the minus sign indicates that the velocity is directed downstream). Finally, from the definition of the pressure coefficient for an incom­pressible, inviscid flow, on the surface of the cylinder:

Cp = 1 – – V4 = 1 – 4 sin2 0. V 2

Physically, a fluid particle approaching the cylinder along the x-axis decelerates to zero velocity at the upstream stagnation point. The particle next accelerates along the cylinder surface (recall that the flow is inviscid) until it reaches a velocity twice the freestream value at the top of the cylinder; it then decelerates along the rear half of the cylinder until it reaches a zero velocity at the rear stagnation point. The pressure coefficient has a value of +1.0 at the stagnation points and -3.0 at the top and bottom of the cylinder. Integration of the pressure (or pressure coefficient) dis­tribution on the surface of the cylinder yields zero lift and drag, a conclusion argued previously from symmetry.

example 4.11 Given: Consider the steady, incompressible, inviscid flow around a cylinder with zero lift.

Required: Predict the points on the upstream side of the cylinder where the sur­face static pressure is equal to the static pressure of the oncoming freestream.

Approach: The pressure-coefficient definition and the equation for the variation of pressure coefficient around the cylinder is used.

Solution: From Eqs. 4.27 and 4.44, with p set equal to pM at the point in question:

Cp = (p p~) = 0 = 1 -4sin20^0 =±30°, ±150°.

p iPV-2

Because the angle is the polar angle measured from the positive x-axis, the required points are at 0 = 150° and 0 = 210° on the upstream side of the cylinder.

Appraisal: The flow streamline along the x-axis stagnates on the cylinder at 0 = 180°. The flow on the surface of the cylinder (i. e., along that same stream­line) then accelerates and, from the Bernoulli Equation, as the velocity (i. e., dynamic pressure) increases, the static pressure must decrease. At a distance
along the surface of only 1/12 of the cylinder diameter, the pressure on the sur­face decreased from a maximum of freestream stagnation pressure to a value equal to the freestream static pressure. Continuing to the top of the cylinder, the velocity increases to a maximum and the static pressure on the cylinder reaches a minimum. The flow field around the cylinder is symmetric, with the freestream static pressure occurring on the surface of the cylinder at mirror-image points in both the x- and у-axes; only the locations on the upstream side of the cylinder were required.