Viscous Fluid Flow and Laminar Boundary Layers

8.1 Incompressible 2-D Flows

Viscous stresses are important in studying aerodynamics and calculating the forces. So far, we have ignored the viscous stresses compared to the pressure and acceleration in the so called inviscid flow in the region outside the viscous layers (around the body and in the wake) (Fig. 8.1).

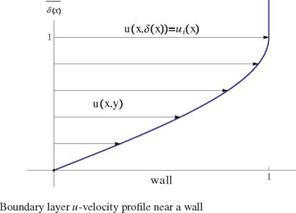
In the neighborhood of the solid surface, the flow slows down and the relative velocity is zero on the surface because of viscosity (no slip condition). The velocity profile u(y) is shown in the sketch, Fig.8.2. Note that in this chapter we will use a local coordinate system with x the curvilinear abscissa along the profile and y the normal distance to the wall, with unit vectors (i, j). Note also that the velocity components u and v represent the full velocity, not just the perturbations from the undisturbed flow.

The friction drag per unit span, Df is given by the shear stress т integrated over the area:

where a is the viscosity coefficient and tw is the component of the shear stress at

the wall in the direction of the incoming flow.

In general a is a function of temperature and slightly depends on pressure. It can be assumed constant for low and moderate speeds.

In our study, we will consider the flow to be laminar; transitional and turbulent flows are more complicated and little is known, in this regard, for practical applica­tions. Therefore, the Reynolds number, Re — in our study is limited. Laminar separated flows will be discussed, and the effect of pressure gradient (retarding the flow) leading to stall (less lift and more drag) will be emphasized.

© Springer Science+Business Media Dordrecht 2015 261

J. J. Chattot and M. M. Hafez, Theoretical and Applied Aerodynamics,

DOI 10.1007/978-94-017-9825-9_8