Our heavyweight helicopter equal in the world does not have
In Rostov started production of the most load-lifting rotary-wing car The Russian holding «Helicopt[...]
Boundary layer equations
Applying all the TSL approximations above to the full Navier-Stokes momentum equation (1.36), and using the unmodified mass equation (1.33), produces the following simpler boundary layer equations.
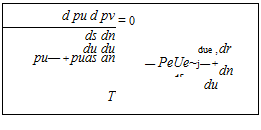(4.21)
In the shear t definition above, pt(s, n) is the Boussinesq eddy viscosity. This captures the effects of turbulence, as will be discussed in the next section.
 |
Appropriate boundary conditions at every s location for a wall boundary layer are
where the boundary condition “at infinity” is now imposed as a specified ue at the edge location ne just outside the boundary layer. The boundary layer equations (4.21) also apply for other shear layer flows such as jets, wakes, and mixing layers. But for these flows different boundary conditions would be used.
If the outer potential flow is incompressible, and in addition there is no significant wall heating or cooling, then the boundary layer is also incompressible and the viscosity is constant, as discussed in Section 1.8. Specifically, in the boundary layer equations (4.21) we have p = pe = constant and p = constant. If pt is also known via some turbulence model, these equations are then closed, meaning that they are solvable for the u, v(s, n) velocity fields.
If significant wall cooling or heating is present, or if the edge Mach number is sufficiently large for significant frictional heating to occur, then the density and viscosity variation across the boundary layer need to be accounted for via the temperature variation. These compressibility corrections are somewhat beyond scope and will not be treated here in any theoretical detail.
