Image Registration

The intensity-based method for PSP and TSP requires a ratio between the wind-on and wind-off images of a painted model. Since a model deforms due to aerodynamic loads, the wind-on image does not align with the wind-off image; therefore these images have to be re-aligned before taking a ratio between the images. The image registration technique, developed by Bell and McLachlan (1993, 1996) and Donovan et al. (1993), is based on an ad-hoc transformation that
maps the deformed wind-on image coordinates (xon, yon) onto the reference wind-off image coordinates (xoff, yof ). In order to register the images, some black fiducial targets are placed on a model. When the correspondence between the targets in the wind-off and wind-on images is established, a transformation between the wind-off and wind-on image coordinates of the targets can be expressed as

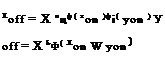(5.27)

The base functions ф(^) are either the orthogonal functions like the Chebyshev functions or the non-orthogonal power functions ф(х) = x1 used by Bell and McLachlan (1993, 1996) and Donovan et al. (1993). Given the image coordinates of the targets placed on a model, the unknown coefficients atj and btj can be determined using least-squares method to match the targets between the wind-on and wind-off images. For image warping, one can also use a 2D perspective transform (Jahne 1999)

ai1Xon + ai2y0n + ai3 a31 Xon + a32 yon + 1

a21 Xon + a22 yon + a23 a31Xon + a 32 y on + 1

Although the perspective transform is non-linear, it can be reduced to a linear transform using the homogeneous coordinates. The perspective transform is collinear that maps a line into another line and a rectangle into a quadrilateral. Therefore, Eq. (5.28) is more restricted than Eq. (5.27) for PSP and TSP applications.

Before the image registration technique is applied, the targets must be identified and their centroid locations in images must be determined. The target centroid (xc, yc) is defined as

where і(xi, yi) is the gray level on an image. When a target contains only a few pixels and the target contrast is not high, the centroid calculation using the definition Eq. (5.29) may not be accurate. Another method for determining the target location is to maximize the correlation between a template f(x, y) and the target scene I( x, y) (Rosenfeld and Kak 1982). The correlation coefficient Cfl is defined as

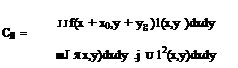For the continuous functions f(x, y) and 1(x, y), one can determine the location (x0,y0) of the target by maximizing Cfl. However, it is found that for small targets in images, sub-pixel misalignment between the template and the scene can significantly reduce the value of Cfl even when the scene contains a perfect

replica of the template. To enhance the robustness of a localization scheme, Ruyten (2001b) proposed an augmented template f(x, y) = f0(x, y) + fxAx + fyAy, where f0(x, y) represented a conventional

template and fx and fy are the partial derivatives of f( x, y ) . The additional shift parameters (Ax, Ay) allowed more robust and accurate determination of the target locations.

In PSP and TSP measurements, operators can manually select the targets and determine the correspondence between the wind-off and wind-on images. However, PSP and TSP measurements with multiple cameras in production wind tunnels may produce hundreds or thousands of images in a given test; thus, image registration becomes very labor-intensive and time-consuming. It is non-trivial to automatically establish the point-correspondence between images taken by cameras at different viewing angles and positions. This problem is generally related to the epipolar geometry in which a point on an image corresponds to a line on another image (Faugeras 1993). Ruyten (1999) discussed the methodologies for automatic image registration including searching targets, labeling targets and rejecting false targets. Unlike ad-hoc techniques, the searching technique based on photogrammetric mapping is more rigorous. Once cameras are calibrated and the position and attitude of a tested model are approximately given by other techniques (such as accelerators and videogrammetric techniques), the targets in the images can be found using photogrammetric mapping from the 3D object space to the image plane (see Section 5.1).

The aforementioned methods of using a single transformation for the whole image is a global approach for image registration. A local approach proposed by Shanmugasundaram and Samareh-Abolhassani (1995) divides an image domain into triangles connecting a set of targets based on the Delaunay triangulation (de Berg et al. 1998). For a triangle defined by the vertex vectors Rj, R2 and R2, a point in the plane of the triangle can be described by a vector u2 Rj + U2 R2 + u3 R3, where (Uj, u2,u3) are referred to as the parametric (barocentric) coordinates and a constraint uj + u2 + u3 = 1 is imposed. When a wind-on pixel is identified inside a triangle and its parametric coordinates is given, the corresponding wind-off pixel can be determined by using the same parametric coordinates in the vertex vectors of the corresponding triangle in the wind-off image. Finally, the image intensity at that pixel is mapped from the wind-on

image to the wind-off image. This approach is basically a linear interpolation assuming that the relative position of a point inside a triangle to the vertices is invariant under a transformation from the wind-on image to the wind-off image. Weaver et al. (1999) proposed a so-called Quantum Pixel Energy Distribution (QPED) algorithm that utilizes local surface features to calculate a pixel shift vector using a spatial correlation method. The local surface features could be targets, pressure taps, and dots formed from aerosol mists in spraying on a basecoat. Similar to particle image velocimetry (PIV), the QPED algorithm can give a field of the displacement vectors when the registration marks or features are dense enough. Based on the shift vector field, the wind-on image can be registered. Although the QPED algorithm is computationally intensive, it can provide the local displacement vectors at certain locations to complement the global image registration techniques. A comparative study of different image registration techniques was made by Venkatakrishnan (2003).