MODIFICATION OF THE RIGID BODY EQUATIONS

Although the inertia terms of the previous equations, for example, (4.9,18) and (4.9,19), remain unchanged to first order by the presence of elastic motions, the elas­tic and rigid-body motions are not nevertheless entirely uncoupled.

The deformations of the structure in general cause perturbations in the aerody­namic forces and moments. These may be introduced into the linearized equations of motion by the addition of appropriate derivatives to the expressions for the aerody­namic forces given by (4.9,17). For example, the added terms in the pitching moment associated with the nth elastic degree of freedom would be

Meen + Mten + Mten (4.12,2)

Similar expressions appear for each of the added degrees of freedom, and in each of the aerodynamic force and moment equations. An example of the elastic stability de­rivatives is given in Sec. 5.10. Alternatively, the aerodynamic forces may be formu­lated in the form of transfer functions.

THE ADDITIONAL EQUATIONS OF MOTION

The additional equations are most conveniently found by using Newton’s laws as ex­pressed by Lagrange’s equations of motion (Synge and Griffith, 1942) with the en as

‘The eigenfunctions of the linear vibration problem.

generalized coordinates. The appropriate form of Lagrange’s equation for this appli­cation is

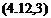d дТ ЭТ dU _ ^

dt дєп дєп дє„ "

where Т is the kinetic energy of the elastic motion relative to FB, U is the elastic strain energy, and SFn is the generalized external force. Since the coordinates are mea­sured in the frame FB, which is non-Newtonian by virtue of its general motion, an ap­propriate modification must be made to the external force field acting on the system when calculating the generalized force. This consists of adding to each element of mass 8m an inertial body force equal to — a’ 8m where a’ is that part of the total ac­celeration of 8m that arises from the acceleration and rotation of FB (see Appendix A.6).

Since normal modes have been chosen as the degrees of freedom, then the indi­vidual equations of motion are independent of one another insofar as elastic and iner­tia forces are concerned (this is a property of the normal modes), although the equa­tions will be coupled through the aerodynamic contributions to the SFs. The lack of elastic and inertia coupling permits the left-hand side of (4.12,3) to be evaluated by considering only a single elastic degree of freedom to be excited. Let its generalized coordinate be en. The kinetic energy is given by

T = J (x’2 + y’2 + z’2) dm

where the integration is over all elements of mass of the body. From (4.12,1) this be­comes (with only e„ excited)

F = hi2 j (f2 + g2 + h2) dm

The integral is the generalized inertia in the nth mode, and is denoted by

In = j(f2n + g2„ + h2n)dm (4.12,4)

so that

T = HA (4.12,5)

The first term of (4.12,3) is therefore I„en, and the second term is zero.

The strain-energy term is conveniently evaluated in terms of the natural fre­quency of the nth mode by applying Rayleigh’s method. This uses the fact that, when the system vibrates in an undamped normal mode, the maximum strain energy occurs when all elements are simultaneously at the extreme position, and the kinetic energy is zero. This maximum strain energy must be equal to the maximum kinetic energy that occurs when all elements pass simultaneously through their equilibrium position, where the strain energy is zero. Hence, if e„ = a sin wnt, then the maximum kinetic energy is, from (4.12,5)

= Lola2

Since the stress-strain relation is assumed to be linear, the strain energy8 is a qua­dratic function of e„; that is, U = ke^r Hence

tfma* = 2 ka2 = 7max = hlnco2na2

It follows that к = Ina>2, and that

U =

and hence dU/den = Inu>len. The left side of (4.12,3) is therefore as follows:

hK + 1 nofen = 3%, (4.12,6)

When structural damping is present, this simple form of uncoupled equation is not exact but the changes in frequency and mode shape for small damping are not large. Hence damping can be allowed for approximately by adding a damping term to

(4.12,6) , that is,

К + 2£>ne„ + w2„en = 9JIn (4.12,7)

without changing wn or the mode-shape functions. The value of £ is ordinarily less than 0.1, and usually must be found by an experimental measurement on the actual structure.

EVALUATION OF

The generalized force is calculated from the work done during a virtual displacement,

dW

3%, = 3- (4.12,8)

de„

where IV is the work done by all the external forces, including the inertia forces asso­ciated with nonuniform motion of the frame of reference. The inertia force field is given by

dt,= -(u’)dm (4.12,9)

where the components of the r. h.s. in FB are given by (A.6,8) without the terms (x, y, z). The work done by these forces in a virtual displacement of the structure is

SWi = I (8x dfx. + 8y dfy. + 8z dfz.)

where the integration is over the whole body. Introducing (4.12,1) this becomes

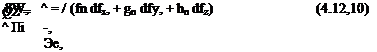і = X Sc, J (fn dfx, + Sn dfy, + К dfz)

When the inertia-force expressions are linearized to small disturbances, and substi­tuted into (4.12,10), all the remaining first-order terms contain integrals of the fol­lowing types:

‘For example, in a spring of stiffness к and stretch x, the strain energy is U = kx2.

f fn dm, J (yh„ – Zgn) dm

The first of these is zero because the origin is the mass center, and the second is zero because the angular momentum associated with the elastic mode vanishes. The net result is that 3F„. = 0. This result simply verifies what was stated above; that is, there is no inertial coupling between the elastic and rigid-body degrees of freedom.

The remaining contribution to??,, is that of the aerodynamic forces. Let the local normal-pressure perturbation at an element dS of the airplane’s surface be p(x0, y0, Zq), and let the local outward normal be n(nx, ny, nz). Then the work done by the aero­dynamic forces in a virtual displacement is

SWa = – j pn-(r – r0) dS

where the integral is over the whole surface of the airplane, and (r – r0) is the vector displacement at dS. It is given by

oo

Г – 1*0 = z (*/» + j8n + кhn) 8en

swa = ~ X 8e" P(nJn + «v?» + nzK) dS n= 1

and

‘dfn = = – f p(nj„ + nyg„ + nzhn) dS (4.12,11)

ОЄп

Each of the variables inside the integral is a function of (jc0, y0, z()), i. e., of position on the surface, and moreover, p is in the most general case a function of all the general­ized coordinates, of their derivatives, and of the control-surface angles. The result is that 3Fn is a linear function of all these variables, which may be expressed in terms of a set of generalized aerodynamic derivatives (or alternatively aerodynamic transfer functions), namely,

3%, = AnuAu + Апйй + • ■ • + Anpp + • • • + AnS8r + ■■■

+ X anmem + X bnm^m + X Cnntm (4.12,12)

m—I m=1 m= 1

In application, only the important derivatives would be retained in any given case. The values of the derivatives kept would be computed by application of (4.12,11). An example of this computation is given in Sec. 5.10.

RESUME

The effects of structural dynamics on the stability and control equations can be incor­porated by adding structural degrees of freedom based on free normal modes. For an exact representation, an infinite number of such modes are required; however, in

practice only a few of the lowest modes need be employed. The six rigid-body equa­tions are altered only to the extent of additional aerodynamic terms of the type given in (4.12,2). One additional equation is required for each elastic degree of freedom

(4.12,7) . The generalized forces appearing in the added equations contain only aero­dynamic contributions, which are computed from (4.12,11) and expressed as in (4.12,12).