Problem Formulation for the Flow Past a Lifting Surface in Proximity to a Solid Boundary

1.2 Formulation of the Three-Dimensional Unsteady Flow Problem

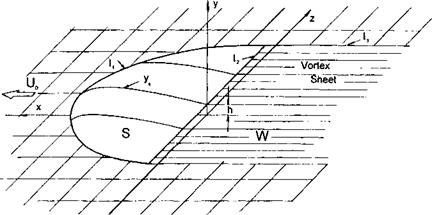
Consider a wing of small thickness and curvature, performing an unsteady motion above a solid nonplanar underlying surface in an ideal incompressible fluid[5] (see Fig. 2.1). Assume that motion of the wing is the result of super­position of the main translational motion with variable speed U(t) and small vertical motions due to heave, pitch, and possible deformations of the lifting surface. Introduce a moving coordinate system in which the axes x and z are located upon an unperturbed position of the underlying boundary (the ground). Axis x is directed forward in the plane of symmetry of the wing, and axis у is directed upward and passes through the trailing edge of the root chord.

In what follows, all quantities and functions will be rendered nondimen­sional by using the root chord C0 and a certain characteristic speed U0. De­fine the relative ground clearance h0 as the ratio of the characteristic dis­tance of the trailing edge of the wing’s root section from the unperturbed position of the ground to the length of the root chord. Introduce functions t/u(x, z, t), y(x, z, t), yg(x, z, t), and yw(x, z,t), characterizing, respectively, the instantaneous positions of the upper and lower surfaces of the wing, the surfaces of the ground, and the wake from the plane у — 0.

Introduce a small parameter є, characterizing a perturbation (for example, angle of pitch, curvature, thickness, amplitude of oscillations or deformations of the wing, deformation of the ground surface, etc.).

With the intention of developing an asymptotic theory valid in close prox­imity to the ground, suppose that the relative ground clearance is small, that is, h0 1. Assume that at any moment the instantaneous distances of points of the wing, wake, and ground surfaces from the plane у = 0 are of the same order as h0 and are changing smoothly in longitudinal and lateral directions. Thus, if y(x, z,t) describes either of these surfaces, then

(!”l’S)=o(£)=ow<<L <2л)

It should be noted that in the case of the extreme ground effect, the assump­tion adopted є = O(h0) does not mean that flow perturbations are necessarily small. It will be shown later on that in the extreme ground effect, the input of the order of О(є) can result in the system’s response of the order of 0(1).

The inviscid incompressible flow around a wing in the ground effect is governed by the three-dimensional Laplace equation and is subject to

• the flow tangency condition on the surfaces of the wing and the ground,

• the dynamic and kinematic conditions on the wake surface (pressure and normal velocity should be continuous across the wake), and

• the decay of perturbations at infinity.

The Kutta-Zhukovsky requirement of pressure continuity can be specified at the trailing edge, although it is automatically satisfied through the boundary conditions on the wake surface.

With this in mind, one can write the following flow problem formulation with respect to the perturbation potential

dx2 dy2 + dz2 ’

ftp = <ty _ u(fs] %.,! dip dyUti %,,!

dy Idx UJ dx dz dz dt ’

У = yu,(x, z,t), (x, z)eS; (2.3)

_ Гrr/#xl дУе, dipdyz, dyg. dx dx + dz dz + dt’

y = yg(x, z,t), (x, z) Є G; (2.4)

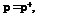
(Vipn) =(Vipn) + , y = yw(x, z,t), (x, z) £ W; (2.5)

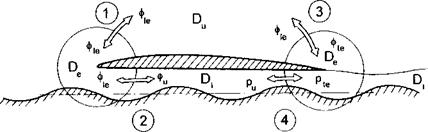
Fig. 2.2. Scheme of subdivision of the flow into characteristic zones and the se­quence of asymptotic matching.

—> 0, x2 + y2 + z2 -> oo, (2.6)

where 5, G, and W are the areas of the wing, the ground, and the wake related to the square of the root chord.

According to the technique of matched asymptotics, the flow domain will be subdivided into the following subdomains with different characteristic length scales (see Fig. 2.2, where, for simplicity, the subdivision is illustrated in two dimensions):

• the upper flow region Du above the wing, its wake and part of the ground outside the projection of the wing and the wake upon the unperturbed ground plane;

• the channel (lower) flow region D under the wing and the wake;

• the edge flow regions De in the vicinity of the edges of the lifting surface and the wake.

In each of the regions, asymptotic solutions of the problem (2.2)-(2.6) are constructed for h0 —» 0 in appropriately scaled coordinates.

The asymptotic matching and additive composition of these solutions en­able accounting for the interaction of different parts of the flow and obtaining a uniformly valid solution for the entire flow domain. In what follows, con­sideration is restricted to the asymptotic accuracy of the order of O(h0).