The и Derivatives (CXu, CZu, CmJ

The и derivatives give the effect on the forces and moments of an increase in the for­ward speed, while the angle of attack, the elevator angle, and the throttle position re­main fixed. If the coefficients of lift and drag did not change, then this would imply an increase in these forces in accordance with the speed-squared law, i. e.,

Since the pitching moment is initially zero, then, so long as Cm does not change with u, it will remain zero. The situation is actually more complicated than this, for the nondimensional coefficients are in general functions of Mach number and Reynolds number, both of which increase with increasing u. The variation with Reynolds num­ber is usually neglected, but the effect of Mach number must be included.

The thrust effect shows up in two different ways. One stems simply from the de­rivative of thrust with speed, which depends on the type of propulsive system-jet, propeller, and so forth. The other, related mainly to propeller configurations, derives from the propulsion/airframe interaction, for example, the propeller slipstream im­pinging on the wing. This is an important effect, and for some STOL airplanes, may be dominant at low speeds.

Finally, the increased loading on the airframe due to the speed increase may in­duce significant structural distortion. This is a static aeroelastic effect. For example, the tail lift coefficient may be influenced appreciably by the loading (see Sec. 3.5). An appropriate variable to use for aeroelastic effects is the dynamic pressure pd =

In order to formally include each of these three major effects, compressibility, aeroelasticity, and propulsive, even though they would rarely all be present at the same time, each of the coefficients Cx, Cz, Cm is assumed to be a function of M, pd, and CT as well as angle of attack.

We then have

(5.3,1)

and similarly for CZu and Cmu.

CALCULATION OF дМІдй

Since the direct aeroelastic effect on thrust is likely to be negligible, we neglect dCT/dpd, and then (5.3,5) gives

When a powered wind-tunnel model is tested, it is common practice to measure the net axial force coefficient Cx and not its component parts C, and CD. In that case, the test data can provide the CXu derivative directly.

THE DERIVATIVE CZu

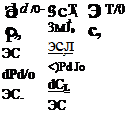From (5.1,1) we have that

The derivative М0(ЭС,/ЭМ0) tends to be small except at transonic speeds. Theoretical values are easily calculated for high-aspect-ratio swept wings. At subsonic speeds, the Prandtl-Glauert rule combined with simple sweep theory (Kuethe and Chow, 1976) gives the lift coefficient for two-dimensional flow as

where a, is the lift-curve slope in incompressible flow and A is the sweepback angle of the і chord line. Upon differentiation with respect to M, we get

dCL M2 cos2 A

M “ ~ =———- 5— 7— C,

ЭМ 1 — M2 cos2 Л

/ dCL Mo cos2 Л

0 ЭМ j0 1 — Mo cos2 Л ^’Lo

In level flight with the lift equal to the weight, MlCLo is constant, and hence М0(ЭС^/ЭМ)0 is proportional to 1/(1 — M2, cos2 Л). At supersonic speeds, the two-di­mensional lift is given by Kuethe and Chow (1976)

4a cos Л
VM2 cos2 A – 1

After differentiation with respect to M, we get exactly the same result as for subsonic speeds. That is (5.3,13) applies over the whole Mach-number range, except of course near M = 1 where the cited airfoil theories do not apply. Low-aspect-ratio wings are less sensitive to changes in M.

THE DERIVATIVE Г

mu

From (5.3,5) and (5.3,6) Cmu is given as

Values of dCJdM can be found from wind-tunnel tests on a rigid model. They are largest at transonic speeds and are strongly dependent on the wing planform. The main factor that contributes to this derivative is the backward shift of the wing center of pressure that occurs in the transonic range. On two-dimensional symmetrical wings, for example, the center of pressure moves from approximately 0.25c to ap­proximately 0.50c as the Mach number increases from subsonic to supersonic values. Thus an increase in M in this range produces a diving-moment increment; that is, СШи is negative. For wings of very low aspect ratio, the center of pressure movement is much less, and the values of Cmu are correspondingly smaller.

To find ЭC„/dpd requires either an aeroelastic analysis or tests on a flexible model. As an example of this phenomenon, let us consider an airplane with a tail and a flexible fuselage.2 We found in Sec. 3.5 that the tail lift coefficient is given by

2It is not meant to imply that fuselage bending is the only important aeroelastic contribution to Cm . Distortion of the wing and tail may also be important.

When (5.3,15) is differentiated with respect to pd and simplified, and the resulting ex­pression is substituted into (5.3,16), we obtain the result

dCm = ka, S,__

fa /.ail "" 1 + ka, PA

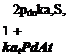The corresponding contribution to Cmu is [see (5.3,14)]

All the factors in this expression are positive, except for Cmt, which may be of either sign. The contribution of the tail to Cmu may therefore be either positive or negative. The tail pitching moment is usually positive at high speeds and negative at low speeds. Therefore its contribution to Cmu is usually negative at high speeds and posi­tive at low speeds. Since the dynamic pressure occurs as a multiplying factor in

(5.3,18) , then the aeroelastic effect on Cmu goes up with speed and down with altitude.