Two-Dimensional Airfoils

5.1 Introduction

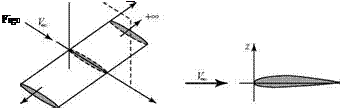
A flight vehicle is sustained in the air by the lift that is generated on the wings. If the vehicle design is to be successful, this lift must be generated as efficiently as possible—that is, with minimum drag and structural weight. Because of their enor­mous importance, wings (and the airfoil sections that comprise them) have been studied for years both experimentally and analytically. The emphasis in this chapter is on flow about airfoil shapes in two dimensions. Two-dimensional flow implies that the flow field and the body shape are identical in any vertical plane aligned with the flow. Thus, an airfoil section at any spanwise station of an infinite wing of constant section (Fig. 5.1a) behaves as if it were in two-dimensional flow (Fig. 5.1b).

If a lifting wing has a finite span band, hence, wing tips at values of,

then there is a flow around the wing tips from the lower surface (i. e., higher pressure) to the upper surface (i. e., lower pressure). The intensity of the spanwise flow due to this effect varies across the wing span, so that the flow field is no longer the same at every spanwise (y) station. The finite wing, therefore, constitutes a three-dimensional flow problem (see Chapter 6).

The focus of this chapter is the prediction of the pressure distribution, lift forces, and moments on various airfoil shapes as well as the dependence of these quantities on airfoil-shape parameters. Initially, no viscous forces are accounted for explicitly; therefore, no drag occurs on a two-dimensional shape. This result is known as D’Alembert’s Paradox, and its origin can be identified readily in the cal­culations in Chapter 4 that describe the lift generation on a cylinder with circulation. Modification of the pressure distribution by three-dimensional flow effects and by viscous forces leads inevitably to drag.

Airfoil shapes are defined by mathematical techniques or by prescribing the values of the shape parameters. The emphasis then is on the so-called direct problem. That is, given the airfoil shape, we find the pressure distribution and the force and moment behavior of the airfoil with angle of attack. The direct problem is investi­gated by experiment, by exact or approximate theories, and—in recent years—by numerical analysis.

Recently, the inverse problem has received considerable attention. That is, given the desired chordwise pressure distribution, we find the airfoil shape that leads to this distribution. The motivation for this approach is control of the behavior of the boundary layer on the airfoil surface relative to transition and separation. Stream – wise pressure gradients have a major effect on the growth and stability of a viscous boundary layer. This suggests that it is desirable to specify the chordwise pressure distribution on the airfoil and then find the airfoil geometry that would generate this pressure distribution. Thus, the airfoil shape is compatible with the desired boundary-layer development. This method allows significant decreases in drag and optimization of other airfoil characteristics. Numerical analysis provides a powerful technique for solving this type of problem; hence, computational methods now have a major role in modern airfoil design.

It is not possible to cover here, in detail, all of the many approaches used in the analysis of airfoils; rather, the objective is to provide a strong framework within which the student readily can access particular techniques in later study. Therefore, the chapter is organized as follows: First, airfoil shape and behavior parameters are defined. Then, the primary focus is to solve the direct problem of determining pressure distribution, forces, and moments on a specified airfoil shape. This development begins with an example of a classical technique for determining the shape and per­formance of an airfoil of arbitrary thickness ratio by an analytical method. Following this, the experimental performance assessments carried out by the National Advisory Committee for Aeronautics (NACA; now NASA) using systematic shape variations are explained. Next, thin-airfoil theory is developed for the prediction of forces and moments on airfoils of arbitrary (but thin) shapes. Thin-airfoil theory is considered in detail because this analysis provides excellent insight into the role of airfoil param­eters and geometry on their aerodynamic performance. The chapter concludes with a brief discussion of numerical methods as applied to the direct problem, as well as comments on modern approaches to the inverse problem with sample results.