ZERO THICKNESS CAMBERED WING AT ANGLE OF ATTACK—LIFTING SURFACES

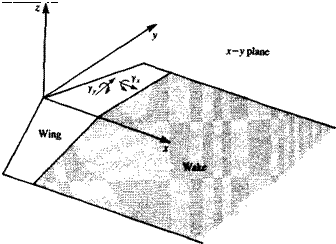
Here we shall solve the two linear problems of angle of attack and camber together (Fig. 4.7). The problem to be solved is

V2<& = 0 (4.29)

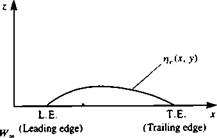
with the boundary condition requiring no how across the surface (evaluated at z = 0) as

(4.41)

This problem is antisymmetric with respect to the z direction and can be

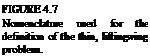solved by a doublet distribution or by a vortex distribution. These basic singularity elements are solutions to Eq. (4.29) and fulfill the boundary condition (Eq. (4.2)) at infinity. As mentioned in Section 2.9, vortex lines cannot begin and terminate in the fluid. This means that if the lifting problem is to be modeled with vortex elements they cannot be terminated at the wing and must be shed into the flow. In order to riot generate force in the fluid, these free vortex elements must be parallel to the local flow direction, at any point on the wake. (This observation is based on the vector product Q«, x Г in Eq. (3.113).)

In the following section two methods of representing lifting problems by a doublet or vortex distribution are presented. Also, as a consequence of the small-disturbance approximation, the wake is taken to be planar and placed on the z = 0 plane.

DOUBLET DISTRIBUTION. To establish the lifting surface equation in terms of doublets the various directional derivatives of the term 1/r in the basic doublet solution have to be examined (see Section 3.5). The most suitable differentiation is with respect to z, which results in doublets pointing in the z direction that create a pressure jump in this direction. Consequently, this antisymmetric point element placed at (x0, y0, Zo) will be used:

The potential at an arbitrary point (x, y, z) due to these elements distributed over the wing and its wake, as shown in Fig. 4.8 (zq = 0), is

Ф (x, y,z) = — _

*rJt Jwing+wake IKX *o)

The velocity is obtained by differentiating Eq. (4.43) and letting z -*• 0 on the wing. The limit for the tangential velocity components was derived in

Section 3.14, whereas the limit process for the normal velocity component is more elaborate (see Ashley and Landahl,41 p. 149).

ЭФ

u(x, y, 0±) = —

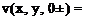
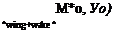
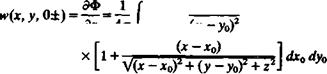
2 ay

(4.44)

To construct the integral equation for the unknown ц(х, у), substitute Eq.

(4.44) into the left-hand side of Eq. (4.41):

J_ f M*o> Уо) L,_____________ (-«–to)_______ 1 . .

43Ї Jwing+wake (У – Уо)* L V(* – X0f + (У~ Уо)* + Z2 ° У0

"«-(£—) <445>

The strong singularity at у – y0 in the integrals in Eqs. (4.44) and (4.45) is discussed in Appendix C.

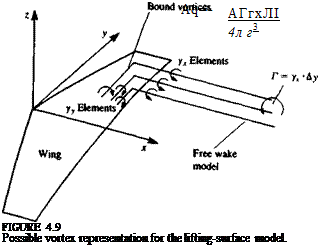
VORTEX DISTRIBUTION. According to this model, vortex line distributions will be used over the wing and the wake, as in the case of the doublet

distribution. This model is physically very easy to construct and the velocity Aq due a vortex line element d with a strength of АГ will be computed by the Biot-Savart law (r is defined by Eq. (4.32)):

Now if vortices are distributed over the wing and wake (Fig. 4.9), then if those elements that point in the у direction are denoted as yy, and in the x direction as yx, then the component of velocity normal to the wing (down – wash), induced by these elements is

. . -i

iK*,y, z)= —

*t71 •’wing+wake

It appears that in this formulation there are two unknown quantities per point (yx, Уу) compared to one (ju) in the case of the doublet distribution. But, according to the Helmholtz vortex theorems (Section 2.9) vortex strength is constant along a vortex line, and if we consider the vortex distribution on the wing to consist of a large number of infinitesimal vortex lines then at any point on the wing дух/ду = Эуу/Эх and the final number of unknowns at a point is reduced to one.

As was shown earlier (in Section 3.14) for a vortex distribution,

beginning at the leading edge (L. E.)
Ф(х, уо, 0±) = f u(xt, yo,0±)dx! •’L. E.	(4.48)
and
ДФ(дг, уо) = Yy(x і, Уо) dx і Jl. e.	(4.49)

The velocity potential on the wing at any point x (y = y0 = const.) can be obtained by integrating the x component of the velocity along an jt-wise line

Yy(x – x0) + yx(y – Уо) [(x-Xof + iy-yof + z2]3*

To construct the lifting surface equation for the unknown y, the wing-induced downwash of Eq. (4.46) must be equal and opposite in sign to the normal component of the free-stream velocity:

Solution for the unknown doublet or vortex strength in Eq. (4.45) or Eq.

(4.50) allows the calculation of the velocity distribution. The method of obtaining the corresponding pressure distribution is described in the next section.