Acknowledgements

I would like to acknowledge Laurent Cordier, Joel Delville, Yves Ger – vais and Bernd Noack, all of whom have contributed to the development of the ideas contained in this document. Anurag Agarwal, Tim Colonius and Jonathan Freund, who continue to stimulate and enrich my general appre­ciation of aeroacoustics, also deserve to be mentioned. Finally, very special thanks are due to Andre Cavalieri and Franck Kerherve, on whose research a good deal of the material contained herein is based.

2 Aeroacoustic theory

In this section we provide a brief presentation of the basic mathematical constructs necessary for an understanding of aeroacoustic theory: the wave equation and its integral solution by means of the free-space Green’s func­tion. This is followed by a detailed exposition of the theory of Lighthill (1952), where its dimensional, statistical and instantaneous representations are used to illustrate some aspects of the relationship between turbulence and sound. The first theoretical evolutions of Lighthill’s theory, due to Phillips (1960) and Lilley (1974), are then evoked, more briefly, followed by a presentation of the most recent theoretical developments, due to Gold­stein (2003) and Goldstein (2005), and which amount to a generalisation of the earlier acoustic analogies. Our exposition of Goldstein’s generalised theory follows the slightly modified formulation proposed by Sinayoko et al. (2011), and we use a model problem computed by these authors in order to illustrate some of the essential aspects of aeroacoustic theory as it pertains to subsonic jets.

e motion of a viscous, compressible, heat-conducting fluid continuum is governed by the equations of mass, momentum and energy conservation, and the equation of state, which are, respectively:

where

represents fluid stresses associated with the thermodynamic pressure, p, and the viscous stresses, т; q is the heat flux due to conduction, given by Fourier’s law, q = —KVT; T is the temperature, s is the entropy, and

Taken together, these equations constitute a closed system of differential equations that governs all classes of motion of a fluid continuum. The
mechanisms that underpin the generation of propagative acoustic energy are contained within this system. However, due to the non-linear nature of the equations, general solutions are not available; and, furthermore, in the general case it is not clear how to: (1) classify motions as turbulent, thermal and acoustic—this classification being possible only in certain limited cases, as shown by Chu and Kovasznay (1958); and, (2) identify clear relationships of cause and effect between different regions of a fluid in motion, or between different kinds of fluctuation of that motion (between velocity and pressure for example).

In acoustics, the situation is considerably simplified, as we focus on one particular class of fluid motion: that which is characterised by small am­plitude fluctuations of a potential nature. In this case it is legitimate to linearise the equations of motion, which reduce, in the case of a quiescent fluid medium, and in the absence of external sources of mass or momentum, to

The velocity perturbation, U, can be eliminated by subtracting the time derivative of the mass conservation equation from the divergence of the momentum conservation equation, giving:

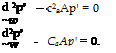p’ and/or p’ can then be eliminated, by means of the constitutive equation p’ = c. p’, to give wave equations in either the density or the pressure: