Acoustic analogies of Phillips and Lilley
A difficulty with the Lighthill analogy, for the problem of jet noise, is that the wave equation describes propagation through a medium at rest. While this model is approximately correct outside the region of turbulent flow, it is not so within the turbulent jet. Two subsequent developments, due to Phillips (1960) and Lilley (1974), were aimed at improving this aspect of
the model. Both were motivated by the desire to explicitly describe effects associated with interactions between the sound field and the jet.
Phillips (1960) proposed an alternative rearrangement of the Navier – Stokes equations, leading to:
d 2n d f 2 dn dui duj d f1 дт – d f 1 ds
dt2 дхі V dx-) dxj dxi dx p dxj ) + dt V Cp dt /
where n = log(p). This equation comprises, explicitly, in the wave operator, some effects of the mean velocity (via the material derivative), in addition to the effects of variable speed of sound that can occur due to temperature or Mach number gradients. The right hand side, which again is considered a source term, comprises, as did Lighthill’s source term, terms associated with non-linear momentum fluctuations, viscous stresses and a term due to entropy unsteadiness.
The modification due to Lilley (1974) comes about from recognising that if we linearise Phillips’ equation about some mean flow, and we consider the fluctuation to be entirely acoustic, the source contains a term associated with flow-acoustic interaction in the form of refraction of the small-amplitude acoustic disturbances by mean shear. To see this, consider acoustic disturbances propagation in two-dimensional shear-flow with mean velocity profile U(y) • x. Linearising Phillip’s equation about this mean flow, and neglecting thermal and viscous effects, the LHS reduces to
![]() 1 d2 p d2p c2o dt2 dx2 ’
1 d2 p d2p c2o dt2 dx2 ’
while the RHS reduces to
When it is possible to verify that the perturbation about the mean flow is indeed an acoustic disturbance, this term describes the refraction of sound by the mean flow, and one can argue that it should appear on the LHS, in the wave operator.
With this in mind, Lilley took the material derivative of Phillips’ equation:
![]() dvA d / о dn dvA dvk dvj
dvA d / о dn dvA dvk dvj
2— ——- ( c2 ) = -2—-—-—- + Ф,
dxi dx – V dxi) dxi dx – dx – ’
 |
||||
where
and we see that by linearising this equation about a base-flow comprising mean shear, we obtain a wave operator that describes acoustic propagation in that shear-flow. It is important to point out however, that a Reynolds decomposition of the velocity field (into U+u), does not correspond to a split into hydrodynamic and acoustic disturbances, and so it is not clear that the linear term so obtained does indeed correspond to a refraction effect in the case of a turbulent jet, where the fluctuation about the time-averaged mean, within the jet, is largely hydrodynamic. This problem of decomposing a flow into acoustic and non-acoustic components lies at the heart of much of the controversy that surrounds acoustic analogy approaches for the description and study of aeroacoustic systems. The most recent attempt to address this difficulty has been proposed by Goldstein (2003) and Goldstein (2005).
2.1 The generalised acoustic analogy
Goldstein (2003, 2005) has shown how the formulations typified by the efforts of Phillips (1960) and Lilley (1974) amount to particular cases in a more general framework. In what follows we provide, firstly, a compact exposition of this generalised formulation, in order to facilitate description and interpretation. We then proceed to give a more complete presentation, following the work of Sinayoko et al. (2011). We end with an overview of a model problem, proposed by these authors, which serves as an instructive illustration of the differences between different acoustic analogy formulations.
In a nutshell Consider the Navier-Stokes equations, expressed in the compact form
N (q) = 0, (36)
where q is here a vector containing all of the dependent flow variables, and N represents the Navier-Stokes operator. Goldstein’s generalisation of the acoustic analogy proceeds as follows.
The full solution is first decomposed into a (possibly unsteady) base-flow and a perturbation:
q = qD + qA, (37)
the subscript D indicating non-linear fluid dynamics, as opposed to linear acoustic dynamics, which are denoted by the subscript A. From this
decomposition an equation of the following form can be written
LqD Ыл) = s(qD)> (38)
where CqD is a linear operator describing the evolution of дл> a disturbance generated and carried by qD. Let us consider this equation for a moment, as it has certain uses, but also some limitations.
A first difficulty associated with an equation constructed in this manner is that, if we are to interpret it in terms of a non-acoustic, causal, source, s(qD), that drives an acoustic effect, дл, we need to be sure that the full flow solution has been decomposed into acoustic and non-acoustic, or radiating and non-radiating, components: there is presently no consensus as to how such a decomposition might be unambiguously effected.
A second difficulty becomes apparent when we consider what has been gained by identifying s(qD) in this way. If we consider equation 38 to be physically pertinent—in other words we believe that we have successfully decomposed the flow solution into acoustic and non-acoustic components— at best we can consider the decomposition of equation 37 to provide us with the kinematic structure of the flow, qD, that underpins sound radiation. However, as we will see in the following example, qD is almost identical to q, the full flow solution, as one would expect given the large amplitude disparity between hydrodynamic and acoustic fluctuations at the heart of the flow; and so the question that arises is the following: in what way does the information provided by decomposition 37 and equation 38 enlighten us with regard to the physical flow mechanisms associated with sound production? The answer appears to be: it constitutes a powerful means by which the radiating flow structure can be visualised and probed. For instance, by superposing s(qD) and qD, and studying, simultaneously, the space-time (or frequency-wavenumber) structure of the two, it may be possible to gain some insight regarding what it was about the flow motions qD that led to the radiating source structure s(qD): this structure (є qD) interacted with that structure (є qD) to produce this or that aspect of the source field (є s(qD)).
However, having clarified the kinematics in this way, it is then necessary to address the question of the dynamics, as the flow motions associated with the generation of sound can only be fully understood in the context of their underlying dynamic law. In the context of high Reynolds number turbulent jets, qD will be no less complex than q, and thus the dynamic law of the source is approximately the Navier-Stokes operator; in which case we arrive at the conclusion that the sound-source mechanism is the turbulence! The point on which we insist is the same evoked in the introduction: while the acoustic analogies can provide simplified models for the propagation
and connection-to-turbulence parts of the problem, they do not directly provide any such simplification where the “fluctuating shearing motions” are concerned. These points will be further discussed in section §3.
Full derivation The following derivation, taken from Sinayoko et al. (2011), shows, in detail, how a generalised acoustic analogy, such as that evoked more compactly above, can be formulated for a homentropic fluid medium. The derivation is followed by the presentation and discussion of a model problem chosen by those authors; the problem considered constitutes a useful illustration of the differences between this and more conventional acoustic analogies; it also serves to illustrate the limitations of acoustic analogies in general.
Using a modified pressure variable п = pl/l, the momentum and energy equations can be rewritten as
Note that the pressure equation now appears in conservative form.
For the moment consider that a filter capable of extracting acoustic, or radiating, disturbances, q’, from the full flow variable, q, exists: L = I-L.
Application of this filter to the conservation equations gives:
![]() др’ d, w
др’ d, w
д + щ {p’> > = 0
д д д
+ dxj >’ + dxn >’ = 0
д (п)’ д.
ow + dx (",J) =0-
The non-linear momentum flux term can be expanded as
pViVj = pViVj + Vj (pvi)’ + Vi(pVj )’ – ViVj p + O(p’2),
where
(PVi) p ‘
O(p’2) terms, being quadratic in the radiating (acoustic variables), are several orders of magnitude smaller than radiating components, and can be neglected. Thus, application of the filter L to the expanded momentum flux term gives
![]() (pViVj)’ & (pViVj)’ +(Vj(pVi)’ + Vi(pVj)’ – ViVjp’)’. A B
(pViVj)’ & (pViVj)’ +(Vj(pVi)’ + Vi(pVj)’ – ViVjp’)’. A B
Term A is the acoustically-matched part of the non-linear momentum flux term, i. e. it comprises only those components of the triple correlation pViVj that present radiation-capable space-time scales, and that can thereby couple with the sound field. The second group of terms, B, corresponds to acoustically-matched components of hydrodynamic-acoustic interaction terms: refraction, scattering, convective transport, etc.
Similarly the modified pressure term, which is also non-linear, can be expanded and filtered:
AB
On account of the homentropic character of the fluid medium, it can be shown (see Sinayoko et al. (2011) for details) that the radiating component
arising due to the non-linearity of the non-radiating pressure term, A, is equal to zero:
Ж)’ = ^(pry f P^Y p)’ = 0. (52)
Р<Ж ПЖ J
Similarly, the energy flux term, (nvj)’, can be decomposed as follows
П П
(nvj)’ – + ( = (pvjУ + v jп – pvjр’)У (53)
A ‘———————- v—————- ‘
B
and the radiating component of the non-linear part shown also to be equal to zero:
(Щ)’ = ^ (pvj)’ = ^ (pvj)’ = 0. (54)
The filtered Navier Stokes equations can now be re-written, placing all of the non-zero sound source terms, A (which comprise radiating components of non-linear interactions of non-radiating components) on the right hand side, and the flow-acoustic interaction terms, B, on the left:
This is a generalised acoustic analogy, the source and propagator components of which depend on how the filter, L is defined.
Application to a model problem We here provide a brief exposition of the model problem and main results. For more complete details the reader should refer to Sinayoko et al. (2011).
A Direct Numerical Simulation is performed wherein a laminar, axisym – metric jet is driven at the inflow by two different frequencies. The response of the jet comprises the growth of two hydrodynamic instabilities; these
|
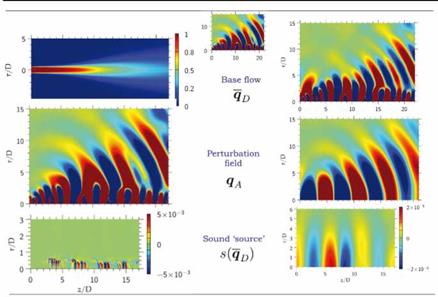
Figure 1. Top center: full flow solution; Left and right columns show, from top to bottom: base flow, perturbation and sound source corresponding to the two flow decompositions; left column :q0 + q"; right column: qD + qA. |
undergo a non-linear interaction which results in a difference wave, and it is this difference wave that dominates the generation of sound waves. The instability waves each couple directly with the sound field, but this linear mechanism is weaker than that of the non-linear interaction.
The full solution of the model problem is shown in figure 1. The filtering operation used to separate ‘radiating’ and ‘non-radiating’ components of the flow is based on the free-space Green’s function, and in this particular implementation the ‘perturbation’ is defined as the radiating component of the flow at the dominant radiation frequency only. It is for this reason that some radiating components remain in the base flow, qD.
The considerable differences between what is referred to as ‘base flow’, ‘perturbation’ and, consequently, ‘source’ are illustrative of the degree to which different acoustic analogies will yield different interpretational frameworks: the mechanisms that we infer from the equations can differ as widely as the decompositions, base-flows, perturbations and sources with which they are associated. Much contemporary debate regarding the true physics
of sound production is fueled by this lack of universality.
We here draw attention to one importance difference in particular. In the case of the time-averaged base flow (which is what is used in Lilley or Linearised Euler formulations), the fluctuation is largely dominated, as stated earlier, by hydrodynamic unsteadiness, whereas the radiating fluctuation obtained by means of an acoustic filter is mainly acoustic. The difference in both amplitude and space-time structure between the two attests to this. As seen in figure 1, when a time-averaged base-flow is considered, the perturbation within the jet is dominated by hydrodynamic, convective scales. When the radiating/non-radiating decomposition is used, the perturbation shows an acoustic (radiating) scale throughout the jet. A corresponding difference in amplitude between the two perturbations (not shown in the figure, where colour scales are saturated) is also observed. This illustrates the extent to which it is incorrect to think of interactions terms of the kind q0q" as corresponding to mean-flow/acoustic interaction; the correct interpretation is that these terms are dominated by mean-flow/turbulence interactions, as is the interpretation attributed to such terms by students of incompressible turbulence (cf. George et al. (1984)), where such terms are referred to as slow-pressure terms.
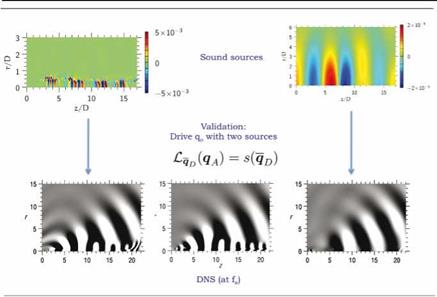
Finally, Sinayoko et al. (2011) verify that when the time-averaged base flow is driven by the two source terms, the correct result is obtained in the acoustic field. Figure 2 shows this.
2.2 Conclusion
Two things are worth pointing out with regard to the results of the model problem considered above. The first is the difference between the two source terms; it clearly cannot be correct to refer to both of these as the ‘source of sound’. Furthermore, because in this model problem the flow has been carefully manipulated so that the fluid dynamics and acoustic mechanisms are clear, we know that the dominant source mechanism comprises a non-linear interaction between two hydrodynamic instabilities; this interaction creates an acoustically-matched difference wave. The source identified by the formulation based on the decomposition into a predominantly non-radiating unsteady base-flow and a monochromatic, purely radiating disturbance resembles such a difference wave. The source obtained using a time-averaged base flow and corresponding disturbance does not. The former system does therefore appear to constitute a more physically pertinent description of the problem than the latter. The causal reading of the problem, as a one way transmission of fluctuation energy from ‘source’ to ‘sound’, also appears to be more justified by the former formulation. As evoked earlier,
|
Figure 2. Result of driving the time-averaged base flow by both sources. Result is compared with the DNS result at the peak acoustic frequency. While the source term constructed from the non-radiating, unsteady base flow elicits a purely acoustic response, the source term associated with the time-averaged base flow causes the mean-flow to respond with both hydrodynamic and acoustic components. Both give the correct result in the acoustic field. |
this improved consistency is also manifest in the response of the base-flow to excitation by the two sources; in the former case the response is purely acoustic, consistent with what has been denoted ‘perturbation’, whereas in the latter case the response is dominated, within the flow, by hydrodynamics: we therefore have a case in the latter situation where the cause is part of the effect and vice versa; this is clearly problematic. It should also be noted, however, that in both cases the correct solution is obtained in the sound field. This shows, as has been borne out over the past 10 years or so by means of numerical simulation, that all acoustic analogies are capable of providing a link between turbulence and sound; however, the differences illustrated by the foregoing study shows that we need to be careful with regard to the physical interpretations that we infer from analysis based on
acoustic analogies.
Where the question of the relationship between qD and s(qD) is concerned, further visualisation and analysis will always be necessary. The same is true with regard to the question of the dynamic law that underpins qD. These observations constitute useful departure points for the experimental approach, and the remainder of these lectures will be concerned with outlining methodologies and tools that can be useful in this regard.