Our heavyweight helicopter equal in the world does not have
In Rostov started production of the most load-lifting rotary-wing car The Russian holding «Helicopt[...]
Backward Difference Stencils
Near the boundary of a computation domain, a symmetric stencil cannot be used; backward difference stencils are needed. Figure 2.10 shows the various 7-point backward difference stencils. Unlike symmetric stencil, the wave number of a backward difference stencil is complex. As will be shown later, a stencil with a complex wave
Figure 2.10. 7-point backward difference stencils for mesh points shown as black circles.
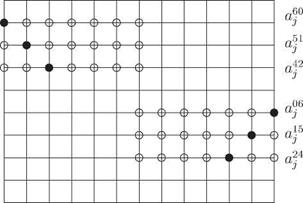number would lead to either damping or amplification depending on the direction of wave propagation. For numerical stability, artificial damping must be added. The subject of artificial damping is discussed in Chapter 7. The following is a set of stencil coefficients that has been obtained through optimization taking into consideration both good resolution and minimal damping/amplification requirements. These backward difference stencils are also useful near a wall or surface of discontinuity.
|
«6° a0 |
= |
«°6 «° |
= |
-2.19228°339°° |
|
«1° |
= |
4«°6i |
= |
4.7486114°1°° |
|
«2° |
= |
-«-2 |
= |
_5.10885191500 |
|
«3° |
= |
-«44% |
= |
4.4615671°4°° |
|
«4° |
= |
-«464 |
= |
-2.833498741°° |
|
«5° |
= |
-«“s |
= |
1.128328861°° |
|
«6° |
= |
-«-б |
= |
_0.20387637100 |
|
fl511 |
= |
– «15 |
= |
_0.20933762200 |
|
«51 a° |
= |
– «15 «° |
= |
_1.08487567600 |
|
«11 |
= |
– «-51 |
= |
2.14777605000 |
|
«21 |
= |
-«-52 |
= |
-1.388928322°° |
|
«31 |
= |
-«-53 |
= |
°.768949766°° |
|
af |
= |
-«-54 |
= |
_0.28181465000 |
|
«51 |
= |
-«-5s |
= |
°.4823°454°°°£ -1 |
|
«-2 |
= |
-«24 |
= |
°.49°41958°°°£ – 1 |
|
«421 |
= |
– «1 |
= |
_0.46884035700 |
|
«42 «° |
= |
_ «24 «° |
= |
_0.47476091400 |
|
«42 |
= |
-«-^ |
= |
1.273274737°° |
|
«22 |
= |
«-2 |
= |
_0.51848452600 |
|
«32 |
= |
«-4? |
= |
°.166138533°° |
|
«442 |
= |
«-4 |
= |
_0.26369431000£ – 1 |
Note: For the three sets of stencil coefficients aj*, a51, and aj2 subscript j = 0 is the stencil point where the derivative is to be approximated by a finite difference quotient. The first superscript is the number of mesh points ahead of the stencil point in the positive direction and the second superscript is the number of mesh points behind.
