Calculation of Forced Response

The formulation of initial-value problems for beams in torsion is almost identical to that for strings, presented in Section 3.1.7. We first should determine the virtual work done by the applied loads, such as a distributed twisting moment per unit length discussed in Section 2.3.1. From this, we may find the generalized forces associated with torsion. Once the generalized forces are known, we may solve the generalized equations of motion, which are of the form in Eq. (3.90). The resulting initial-value problem then can be solved by invoking orthogonality to obtain values

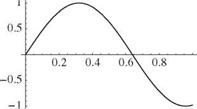
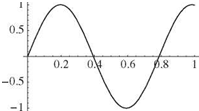
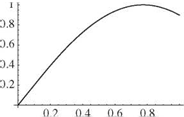
Figure 3.24. First three mode shapes for clamped-spring- restrained beam in torsion, Z = 1

of the arbitrary constants in the general and particular solutions, as illustrated in the examples in Section 3.1.7.

3.3 Uniform Beam Bending Dynamics

The free vibration of a beam in bending is often referred to as “transverse vibration.” This type of motion differs from the transverse dynamics of strings and the torsional dynamics of beams in that the governing equations of motion are of a different mathematical form. Although these equations are different, their solutions are ob­tained in a similar manner and exhibit similar physical characteristics. Again, we start with the properties varying with x and specialize when we must. Observe that whereas most aerospace structures experience combined or simultaneous bending and torsional dynamic behavior, we have here chosen certain configuration variables to uncouple these types of motion.