Determination of Drag
If Pr = 1 (i. e. ЦCp = k), the energy equation in the boundary layer approximation becomes
![]() dT д d u2 d dH
dT д d u2 d dH
д) + dy Ы2 = дУ (M4)
This simplified equation admits a solution H = HTO, provided the boundary conditions on the temperature is consistent with this solution:
At the wall u = 0, hence Tw = HTO/Cp; also,
![]() д T du д T
д T du д T
Cp + u = 0, at the wall |w = 0
d y d y d y
The energy equation is replaced by Bernoulli’s law inside the boundary layer:
where p = pi (x).
Assume that the undisturbed flow is aligned with the x-axis.
The drag per unit span, D’ can be obtained by direct integration of the stresses around the profile as
D = pdy + tw dx (8.68)
where (dx, dy) is a small element of the profile contour C.
From momentum balance applied to a large rectangle surrounding the profile, see Fig. 8.7. Contributions on control surfaces 3 and 4 vanish when the control volume is expanded far away and contributions on 1 and 2 can be combined, resulting in the drag being obtained as an integral across the far wake:
|
/ |
TO
pu(x, y)(U — u(x, y)) dy (8.69)
-TO
The drag can also be evaluated in terms of entropy (Oswatitsch formula [1]).
Assume Pr = 1 and H = H0. Using Crocco’s relation for viscous flows at the far wake:
– U = Tx + viscous term (8.70)
dy dy
Ignoring the last term for high Reynolds number flows in the wake, the above equation gives
![]() – Uu = Txs + const.
– Uu = Txs + const.
Far from the wake, the flow returns to uniform conditions and the entropy to sx. Hence
U(U – u) = Tx(s – sx) (8.72)
The drag reads
T 00
D = U pu(s – sx)dy (8.73)
U – x
The work done by the drag D’U is related to the losses in terms of entropy.
In the case of a flat plate, the drag is simply the friction drag.
In the case of an airfoil, the drag is the sum of friction drag and pressure drag (due to separated flow).
8.2.5 Unsteady Boundary Layer
The unsteady boundary layer equations are given by
![]()
![]()
+ dfi = 0
dt dx dy
dpu du du dpui dui d
~df + pu dx + pv dy = ~dT + pui dX + dy
![]()
|
|
||
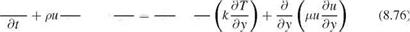
where p = pRT and p = p(T).
The boundary conditions at the solid wall (y = 0) are
![]() u(x, 0) = uw(t), v(x, 0) = 0, T = Tw(x, t)
u(x, 0) = uw(t), v(x, 0) = 0, T = Tw(x, t)
As a simple example of unsteady boundary layer, Liepmann and Roshko [2] discuss the Rayleigh’s problem representing the diffusion of vorticity, see also Schlicht – ing [3] and Howarth [4].













