Example Calculations of Forced Response

In this section, we present two examples of forced-response calculations. These examples also appropriately are called “initial-value problems.” The first has zero initial displacement and velocity; the second has nonzero initial displacement and zero initial velocity.

Example: Calculation of Forced Response. An example of a dynamically loaded uniform string is considered to illustrate the generalized force computation and subsequent solution for the string displacement. The specific example is a uniformly distributed load (in space) of simple harmonic amplitude (in time) shown in Fig. 3.8 with

The generalized force can be determined from the integral of a distributed loading as

rl

/ f (x, t)фі (x)dx Jo

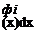
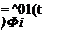
(3.119)

= F01(t )sin

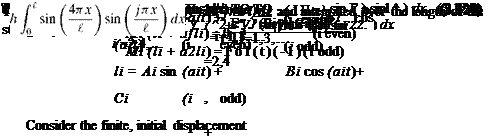because

These integrals can be evaluated easily by noting the orthogonality property of the sine functions. The result gives the following values for the constants Bi:

B4 = h

Bi = 0 (i even but = 4) (3.125)

Bi = – Ci (i odd)

The initial velocity being zero requires that

(x, 0) = £ h (0)Фі (x) = J2 Vi A sin = 0 (3.126)

Multiplication by sin( jnx/l)dx and integration results in determining that Ai = 0 for all i. These results can be summarized by noting that h = 0 for all even values of i except

h4 = h cos (v4t)	(3.127)
and for odd i
hi = Ci [1 – cos (ю-t)] (i odd)	(3.128)
The constants Ci can be determined by substitution of the odd generalized coordinates back into the equations of motion
MiCi= F0(-1)^ t > 0	(3.129)
Given that Mi = mt/2, this yields
C 2Щ(-1) ¥ Ci T(i n )2	(3.130)

so that the complete string displacement becomes v(x, t) = jn hi (t)Фі (x) i =1

і / ■ /4nx 21F0 ^ (-1)1-1 /inx

= h cos (a>4t) sin ^ — j + ТПЇ Z_, — -2 [1 – cos M)] sin ^ — j

(3.131)

Thus, the first term is the response due to initial displacement, and the sum over the odd-indexed modes is the response due to the forcing function.

3.2 Uniform Beam Torsional Dynamics

Although vibrating strings are easy to visualize and exhibit many of the features of vibrating aerospace structures, to analyze such structures, more realistic models are needed. In this section, we apply the concepts related to the modal representation
to the dynamics of beams in torsion. A beam is a structural member in which one dimension is much larger than the other two. It is thus understandable to idealize the twisting and bending of high-aspect-ratio wings and helicopter rotor blades in terms of beam theory, especially in conceptual and preliminary design. Because many behavioral characteristics of typical aeronautical structures are found in beams, the torsion of beam-like lifting surfaces plays a vital role in both static and dynamic aeroelasticity.

3.2.1 Equations of Motion

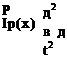For free vibration of a beam in torsion, we specialize the equation of motion derived in Section 2.3.1 by setting r (x, t) = 0 to obtain

Other than the quantities that multiply the partial derivatives, this equation of motion is similar to that for the dynamic behavior of a string. The difference is that the stiffness coefficient GJ (x), unlike the tension in the string, may not be constant. Specialization to the spanwise uniform case is undertaken to obtain a closed-form solution. Properties varying with x are not an obstacle for application of the variety of approximate methods discussed in Section 3.5, but here we are concerned with obtaining closed-form solutions to aid in understanding the results. As shown when we explore the boundary conditions in detail, there are more interesting possibilities for the boundary conditions for beams in torsion than there are for the string.

As before, we apply separation of variables, by substituting

в(x, t) = X(x)Y(t)

into the partial differential equation of motion and arranging the terms so that dependencies on x and t are separated across the equality. This yields

[GJ( x) X 7(x)]7 = Y(0 P Ip(x)X(x) Y(t)

Thus, each side must equal a constant—say, – a>2—so that

[J x) X7 (x)]7 = Щ= _ш2 P Ip(x) X(x) Y(t)

Two ordinary differential equations then follow; namely

[GJ (x) X’ (x)]7 + p Ip(x)a>2 X(x) = 0 Y(t) + a>2Y(t) = 0

The first of Eqs. (3.136) has variable coefficients in x and—except for certain special cases such as spanwise uniformity—does not possess a closed-form solution. The second, however, is the same as the second of Eqs. (3.6), the solution of which is well known.

Some specialization is necessary in order to proceed further. Therefore, we consider only beams with spanwise uniform properties. Eqs. (3.136) then become

X" + a2 X = 0 Y + ш2У = 0

where a2 = pIpu>2/GJ. For a = 0, the solutions can be written as

X(x) = Asin(ax) + B cos(a x) Y(t) = C sin (a>t) + D cos (&t)

To complete the solutions, constants A and B can be determined to within a mul­tiplicative constant from the boundary conditions at the ends of the beam; C and D can be found as a function of the initial beam deflection and rate of deflection. Because the partial differential equations of motion governing both transverse vibra­tion of uniform strings and torsional vibration of uniform beams are one-dimensional wave equations, we rightfully can expect all of the previously discussed properties of standing and traveling waves to exist here as well.

Note that the special case of a = 0 is an important special case with a different set of general solutions. It is addressed in more detail in Section 3.2.3.