Example Solutions for Mode Shapes and Frequencies

In this section, we consider several examples of the calculation of natural frequen­cies and mode shapes of vibrating beams in torsion. We begin with the clamped-free
$ = 0

Figure 3.17. Schematic of clamped-free beam undergoing torsion case, often referred to as “cantilevered.” Next, we consider the free-free case, illus­trating the concept of the rigid-body mode. Finally, we consider a case that requires numerical solution of the transcendental characteristic equation: a beam clamped at its root and restrained with a rotational spring at the tip.

Example Solution for Clamped-Free Beam. To illustrate the application of these boundary conditions, consider the case of a uniform beam that is clamped at x = 0 and free at x = l, as shown in Fig. 3.17. The boundary conditions for this case are

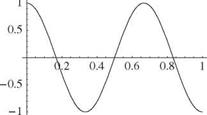
X(0) = X'(l) = 0 (3.165)

Recall that the general solution was previously determined as

в(x, t) = X(x)Y(t) (3.166)

where Xand Y are given in Eqs. (3.138). For a = 0, the first of those equations has the solution

X(x) = Asin(a x) + B cos(a x) (3.167)

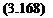It is apparent that the boundary conditions lead to the following X(0) = 0 requires B = 0 X'(l) = 0 requires Aa cos(al) = 0

If A = 0, a trivial solution is obtained, such that the deflection is identically zero. Because a = 0, a nontrivial solution requires that

cos(al) = 0

This is called the “characteristic equation,” the solutions of which consist of a denu – merably infinite set called the “eigenvalues” and are given by

ai l = (2i -1)n (i = 1, 2,…) (3.170)

The Y(t) portion of the general solution is observed to have the form of simple harmonic motion, as indicated in Eq. (3.160), so that the natural frequency is

(3.171)

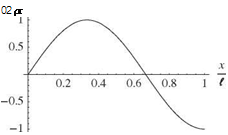
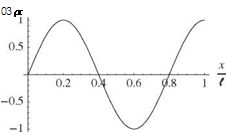
Figure 3.18. First three mode shapes for clamped-free beam vibrating in torsion

Because a can have only specific values, the frequencies also take on specific numer­ical values given by

These are the natural frequencies of the beam. Associated with each frequency is a “mode shape” as determined from the x-dependent portion of the general solution. The mode shapes (or eigenfunctions) can be written as

or any constant times фі (x). The first three of these mode shapes are plotted in Fig. 3.18. The zero derivative at the free end is indicative of the vanishing twisting moment at the free end.

Example Solution for Free-Free Beam. A second example, which exhibits both elastic motion as described previously and motion as a rigid body, is the case of a

ai t = i n (i = 1, 2,…)	(3.178)
and the corresponding natural frequencies become
i n GJ 1 Wp
(3.179)
The associated mode shapes are determined from the corresponding X(x) as
Фі (x) = cos(a;x) = cos t	(3.180)
These frequencies and mode shapes describe the normal mode of vibration for the elastic degrees of freedom of the free-free beam in torsion. Now, if in the previous analysis the separation constant, a, is taken as zero, then the governing ordinary differential equations are changed to
Xl = РІ£Ї = 0 X GJY or
(3.181)
(3.182)
(3.183)
The arbitrary constants, a and b, in the spatially dependent portion of the solution again can be determined from the boundary conditions. For the present case of the

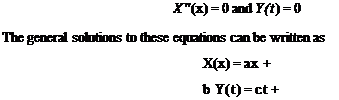free-free beam, the conditions are

X'(0) = 0 requires a = 0 X'(t) = 0 requires a = 0

Because both conditions are satisfied without imposing any restrictions on the con­stant b, this constant can be anything, which implies that the torsional deflection can be nontrivial for a = 0. From X(x) with a = 0, it is apparent that the corresponding value of в is independent of the coordinate x. This means that this motion for a = 0 is a “rigid-body” rotation of the beam.

The time-dependent solution for this motion, Y(t), also is different from that obtained for the elastic motion. Primarily, the motion is not oscillatory; thus, the rigid-body natural frequency is zero. The arbitrary constants, c and d, can be ob­tained from the initial values of the rigid-body orientation and angular velocity. To summarize the complete solution for the free-free beam in torsion, a set of general­ized coordinates can be defined by

в(x, t) = ^2 Фі(x)&(t) (3.185)

і =0

where

Ф0 = 1

The first three elastic mode shapes are plotted in Fig. 3.20. The zero derivative at both ends is indicative of the vanishing twisting moment there. The natural frequencies associated with these mode shapes are

«0 = 0

Note that the rigid-body generalized coordinate, f0(t), represents the radian measure of the rigid-body rotation of the beam about the x axis.

A quick way to verify the existence of a rigid-body mode is to substitute « = 0 and X = a constant into the differential equation, and boundary conditions for X. A rigid-body mode exists if and only if all are satisfied. Caution: Do not try to argue that there is a rigid-body mode because a = 0 satisfies the characteristic equation, Eq. (3.177). To obtain that equation, we presupposed that a = 0!

Example Solution for Clamped-Spring-Restrained Beam. A final example for beam torsion is given by the system shown in Fig. 3.21. The beam is clamped at the root (x = 0) end, and the other end is restrained with a rotational spring having spring constant к = ZGJjt, where Z is a dimensionless parameter. The boundary

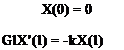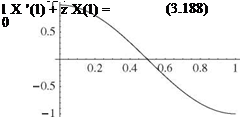conditions on X are thus

When these boundary conditions are substituted into the general solution found in Eqs. (3.138), we see that the first condition requires that B = 0; the second condition, along with the requirement for a nontrivial solution, leads to

Z tan(al) + al = 0

Figure 3.21. Schematic of torsion problem with spring

af

, tan(a^)

z

This transcendental equation has a denumerably infinite set of roots that cannot be found in closed form. However, as many of these roots as desired can be found using numerical procedures found in commercially available software packages such as Mathematical Maple™ and MATLAB™

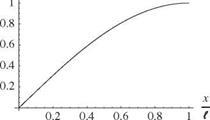
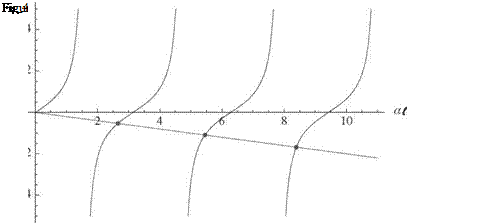
To facilitate this sort of root-finding in general, we may need to specify initial guesses for the values of ai. These can be found using graphical means by plotting, for example, tan(ai) and – ai/Z versus ai for a specified value of Z = 5, as shown in Fig. 3.22. The points where these curves intersect (indicated by dots in the figure) are the solutions, the locations of which are seen to be approximately at ai = 2.6, 5.4, and 8.4. These values, when used as initial guesses in a root-finding application, provide quick convergence to a1i = 2.65366, a2i = 5.45435, and a3i = 8.39135. As an alternative approach for this particular example, we may solve Eq. 3.189 for Z and plot it versus ai to find the roots without iteration.

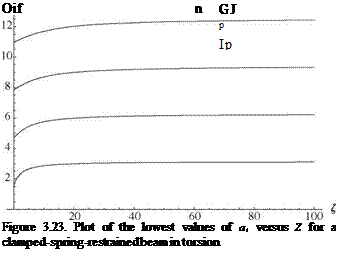
Thus, the roots of Eq. (3.189) are functions of Z, and the first four such roots are plotted versus Z in Fig. 3.23. Denoting these roots by ai, with i = 1, 2,…, we obtain the corresponding natural frequencies

Vi = ai (i = 1,2,…) (3.190)

P Ip

From the plots (and from Eq. 3.189), we note that as Z tends toward zero, a1i tends toward n/2, which means that the fundamental natural frequency is

(3.191)

which is the natural frequency of a clamped-free beam in torsion (as shown herein). We also can show that as Z tends to infinity, a1i tends toward n so that the

fundamental natural frequency is

which is the natural frequency of a clamped-clamped beam in torsion. Recalling the similarity of the governing equations and boundary conditions, the determination of the natural frequencies of a clamped-clamped beam in torsion follows directly from the previous solution for natural frequencies of a string fixed at both ends.

To obtain the corresponding mode shapes, we take the solutions for ai and substitute back into X, recalling that we can arbitrarily set A = 1 and that B = 0. The resulting mode shape is

фі = sin(a^x) (i = 1,2,…) (3.193)

The first three modes for Z = 1 are shown in Fig. 3.24. As expected, neither the twist angle nor its derivative are equal to zero at the tip. Close examination of Fig. 3.24 illustrates that for higher and higher frequencies, the spring-restrained ends behave more and more like free ends.