Inflow/Outflow Representation
We examine the effects of the various parameters defining the cascade geometry and the characteristics of the incident disturbances. We present results for a swirling fbw in a full annulus and study the effects of the cascade threedimensional geometry, radial swirl distribution, reduced frequency, and incident disturbance characteristics on the unsteady aerodynamic forces and the radiated acoustics. These results are used to establish when the nonuniform swirling flow produces significant changes to the aeroacoustic response and to elicit the conditions which affect the magnitude and nature of the scattered field.
For simplicity, we model the mean swirl component as a combination of rigid body rotation and potential vortex swirl,
Г
ив = Пг+~. (15)
r
This model is defined by the two constant parameters ^ and Г. We further assume the ft>w to be isentropic with a uniform enthalpy from hub to tip. In this case, the axial component of velocity is given by
r
U2X =U2m – 2[ff(r2 – r2J + 2 fir ln( —)], (16)
r m
where Um is the axial velocity at the mean radius of the duct rm. It is convenient for presenting the numerical results to define the axial and swirl velocities in terms of the Mach numbers at the mean radius Mm = Um /com,
Mm(Q) — (^rm )/com and Mm( Г) — Г / (r m com ).
We consider the scattering of both incident vortical and acoustic waves. For vortical waves, we take one Fourier component of (5),
umg — Uxmg ex + Urmg er + UOmg eO (17)
As in [Atassi et al., 2004], we introduce the upwash velocity component normal to the streamlines in the x — в plane
where, U — у Ux2 + U|. This facilitates comparison with two-dimensional theory.
Incident acoustic waves are expanded in terms of the normal modes. The mn component of the incident pressure is of the form
and its velocity components are defined in terms of the pressure in [Atassi et al., 2004]. The upwash for the acoustic mode is defined as
„(и) __ „(і) ‘U’xmnUe A tlgmnUx
®mn ^ran jj >
where uxmn and ugmn are the axial and azimuthal acoustic velocity of the {mn} mode, respectively.
We define the sectional lift coefficient as,
where L is the force per unit span and c is the chord length and where we have dropped the subscript for a(u) so that it could represent either a gust (18) or an acoustic wave (20). The quantities po, c, a(u), and U are evaluated at the radial location of the considered section. The acoustic coefficients are calculated so that the maximum value of pressure eigenfunctions are equal to unity and the pressure is normalized by (pomcomam’) where pom, com, and am’ are the values of the mean density, the mean speed of sound, and the upwash at the mean radius, respectively. The calculations are carried out with the ж-axis centered at the mid-chord of the blade (vane) at the mean radius.
Without loss of generality, we can expand the velocity at the section x = x о in terms of a Fourier series,
mg =+Ж
U(v) = £ Wmg (xo, r)ei(mge-Wt). (5)
mg = — ж
Considering one Fourier component, dropping the subscript m g, It was shown in [Atassi et al., 2004] that the vortical upstream disturbances must satisfy
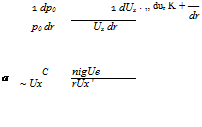 |
|
|
|
|
|
|
|
To facilitate comparison with the two-dimensional theory, it is convenient to introduce the upwash velocity component normal to the streamlines in the x — в plane
/ 4 —ux Ue + Ue Ux
a{u)(r) =——————–
where, U = Ju% + Uq.
We can then express ux and ug in terms of ur and a(u) (r). The radial velocity nr (r) can be chosen arbitrarily but must satisfy the impermeability condition at the hub and the tip.
A quasi-periodic condition is applied in the 9 direction,
Y(x,9e, r)= Y(x, 0,r)eia. (9)
where a = m’9e, 9e = y-, and V is the number of blades (vanes) in the row. All variables upstream of the blades must satisfy this condition. This condition is equally applied to the density and the velocity component normal to the wakes downstream of the blades (vanes). Thus the propagating acoustic waves must satisfy the condition,
m9e = m’9e — 2 qn, (10)
where q is an integer. For a rotor/stator interaction, m’ = pB and hence we arrive at the Tyler and Sofrin Tyler and Sofrin, 1962 condition,
m = pB — qV. (11)
Away from the blade row the farfield behavior of the scattered unsteady disturbances is governed by the eigenmode analysis. To satisfy the causality condition that energy from the source must propagate out of the computational domain, we use the group velocity to segregate the modes propagating downstream (upstream) and denote them with the superscript + (—). Thus we express the unsteady density in the farfield as follows,
where k±n are the axial wave numbers corresponding to the density eigenfunctions V:±n (r). S±n are the sets of all possible values of m.
For computational purpose this condition is truncated and cast in matrix form
P N = [Cn ]c, (13)
where the elements of the vector PN are the unsteady density of the different grid points at the exit plane at x = xN. The elements of the vector c are the coefficients cmn, and the elements of the matrix [Cn ] are the values of the normal modes V+n (ri)ei(kmnXN +m0j) at (i, j).
Similarly, we can write the solution at the previous axial cross-section located at x = xN_i. This provides the following condition,
Pn = [Cn ][Cn _i ]-1Pn _i. (14)
Note that the number of modes used in the expansion may be smaller than the number of grid points of the computational domain.












