Level flight at different air speeds

So far we may seem to have assumed that there is only one condition of level flight; but this is not so. Tevel flight is possible over the whole speed range of the aeroplane, from the maximum air speed that can be attained down to the minimum air speed at which the aeroplane can be kept in the air, both without losing height. This speed range is often very wide on modern aircraft; the maximum speed may be in the region of 1000 knots or even more, and the minimum speed (with flaps lowered) less than 150 knots. Mind you, though level flight is possible at any speed within this range, it may be very inadvis­able to fly unduly fast when considerations of fuel economy are involved, or to fly unduly slowly if an enemy is on your tail! There is nearly always a correct speed to fly according to the circumstances.

Relation between air speed and angle of attack

An aeroplane flying in level flight at different air speeds will be flying at dif­ferent angles of attack, i. e. at different attitudes to the air. Since the flight is level, this means different attitudes to the ground, and so the pilot will be able to notice these attitudes by reference to the horizon (or to the ‘artificial horizon’ on his instrument panel).

For every air speed – as indicated on the air speed indicator – there is a cor­responding angle of attack at which level flight can be maintained (provided the weight of the aeroplane does not change).

Let us examine this important relationship more closely. It all depends on our old friend the lift formula, L = CL. jpV2 . S . To maintain level flight, the lift must be equal to the weight. Assuming for the moment that the weight remains constant, then the lift must also remain constant and equal to the weight. The wing area, S, is unalterable. Now, if we look back, or think back, to Chapter 2 we will realise that TpV2 represents the difference between the pressure on the pitot tube and on the static tube (or static vent), and that this difference represents what is read as air speed on the air speed indicator; in other words, the indicated air speed. There is only one other item in the formula, i. e. CL (the lift coefficient). Therefore if IpV2, or the indicated air speed, goes up, CL must be reduced, or the lift will become greater than the weight. Similarly, if ~_p V2 goes down, CL must go up or the lift will become less than the weight. Now CL depends on the angle of attack of the wings; the greater the angle of attack (up to the stalling angle), the greater the value of CL. Therefore for every angle of attack there is a corresponding indicated air speed.

This is most fortunate, since the pilot will not always have an instrument on which he can read the angle of attack, whereas the air speed indicator gives him an easy reading of air speed. That is why a pilot always talks and thinks in terms of speed, landing speed, stalling speed, best gliding speed, climbing speed, range or endurance speed, and so on. The experimenter on the ground, on the other hand, especially if he does wind tunnel work, is inclined to talk and think in terms of angle, stalling angle, angle of attack for flattest glide, longest range, and so on. This difference of approach is very natural. The pilot, after all, has little choice if he does not know the angle of attack but does know the speed. To the experimenter on the ground, speed is rather meaningless; he can alter the angle of attack and still keep the speed constant – something that the pilot cannot do. But, however natural the difference of outlook, it is unfor­tunate; and it is undoubtedly one of the causes of the gap between the two essential partners to progress, the practitioner and the theorist.

Air speed, metres per second Air speed, knots

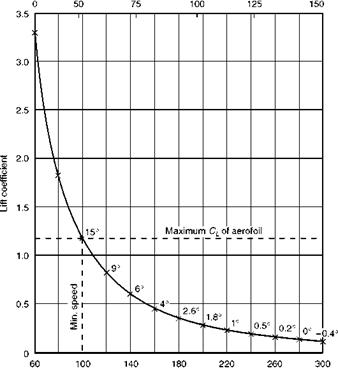
Fig 5.9 Air speed, lift coefficient and angle of attack Aeroplane of weight 50 kN (5100 kgf); wing area 25.05 m2; wing loading 1920 N/m2 (196 kgf/m2); aerofoil section characteristics Figs 3.13, 3.15, 3.16 and 3.17.

Let us examine our general statement more critically by working out some figures. Suppose the mass of an aeroplane is 5100 kg (so that its weight will be approximately 50 000 newtons and that its wing area is 26.05 m2, i. e. a wing loading of about 1920 N/m2. Assume that the aerofoil section has the lift characteristics shown in the lift curve in Fig. 3.13. Consider first the ground level condition, the air density being 1.225 kg/m3.

Whatever the speed, the lift must be equal to the weight, 50 kN; but the

lift must also be equal to CL. ^pV2. S, so

50 000 = С, X – X 1.225 X V2 X 26.05 L 2

from which

CL = 3134/V2

Now insert values for V of 60, 80, 100 and other values up to 300 knots, con­verting them, of course, to m/s, and work out the corresponding values of CL; then by referring to Fig. 3.13 read off the angle of attack for each speed. The result will be something like that shown in Table 5.1 and in Fig. 5.9. The angles given in the table are approximate since all the values are small.

Now let us see what this table and graph mean; we shall find it very inter­esting. In the first place at speeds below about 100 knots, the lift coefficient needed for level flight is greater than the maximum lift coefficient (1.18) pro­vided by the aerofoil, therefore level flight is not possible below this speed. Secondly, as the speed increases to 120, 140, 160 knots, etc., the angle of attack decreases from 15° to 9°, 6°, 4°, etc.; and for each speed there is a cor­responding angle of attack. We should notice, in passing, that at comparatively low speeds there is much greater change in angle of attack for each 20 knots increase in air speed than there is at the higher speeds, e. g. the angle of attack at 120 knots is 6° less than at 100 knots, whereas at 280 knots it is only 0.2° less than at 260 knots. This change in proportion is interesting, and is one of the arguments for an angle of attack indicator, which is sensitive at low speeds, which is just where the air speed indicator is most unsatisfactory.

We could, of course, continue Table 5.1 speeds higher than 300 knots, and we should find that we needed even smaller lift coefficients, and even more negative angles of attack (though never less than 21.8° since at this angle there would be no lift, whatever the speed). But at this stage we must begin to con­sider another factor affecting speed range, namely the power of the engine. What we have worked out so far is accurate enough, provided we can be sure

Table 5.1 Angle of attack derived from airspeed knots Air speed m/s V2 CL = 3134/V2 Angle of attack 60 30.8 949 3.31 – 80 41.2 1697 1.85 – 100 51.5 2652 1.18 15° 120 61.8 3819 0.82 9° 140 72.0 5184 0.60 6° 160 82.4 6790 0.46 4° 180 92.6 8580 0.37 2.6° 200 103.0 10 600 0.30 1.8° 220 113.2 12 800 0.24 1° 240 123.7 15 400 0.20 0.5° 260 134.0 18 000 0.17 0.2° 280 144.0 20 740 0.15 0° 300 154.0 23 700 0.13 -0.4°

of obtaining sufficient thrust. It may be that at speeds of 300 knots or above or, for that matter, at 100 knots or below, we shall not be able to maintain level flight for the simple reason that we have not sufficient engine power to overcome the drag. So the engine power will also determine the speed range, not only the top speed, but also to some extent the minimum speed.

If the reader thinks that the minimum speed of this aeroplane is rather high, we should perhaps point out, first, that we have not used flaps; secondly, that the aerofoil does not given a very high maximum lift coefficient; and, thirdly, that it has a fairly high wing loading, or ratio of weight to wing area, which, as we shall see later, has an important influence on minimum speed. All we wish to establish now is the relationship between air speed and angle of attack, and this is clearly shown by Table 5.1.