Lifting Line Theory

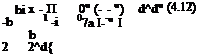The Prandtl’s Lifting Line Theory is valid only for the high aspect ratio wings. For high aspect ratio wings, x — П value can be neglected compared to – — " in first term of the right hand side of Eq. 4.11b. While making this assumption here, we presume that as x approaches П and – approaches ", the vortex sheet strength is not too large. Now, if we use the fact that (- — ")2 is much larger than (x — П)2 we can simplify the double integral in 4.11b as follows

b

Substituting 4.12 into 4.11b we obtain

bi

U0£a = 1 f 7a(n^dn – 1 f dr d"

0x 2л x – П 4л d" – -"

-b – i

In Eq. 4.13, if we neglect the second term at the right hand side we obtain the two dimensional steady state flow relation between the vortex sheet strength and the equation for the profile. The second term, on the other hand, is the contribution

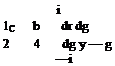of the spanwise circulation change. In order to invert Eq. 4.13 we multiply the equation with J (b + x) /(b — x) and integrate with respect to x we obtain

In two dimensional steady flow the sectional lift coefficient obtained before was

If we compare the left hand side of 4.14 with the right hand side of 4.15, and consider the spanwise dependence also for any section on the wing we obtain

In small angles of attack the sectional lift coefficient is proportional with the angle of attack. This enables us to define the lift line slope as a(y) = 9c/ 9a. The lift coefficient becomes

ci(y) = 88a(y) = a(y)a(y) ^4.17)

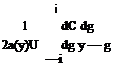Using 4.16 and 4.17 in Eq. 4.14 we obtain the formula for Prandtl’s lifting line theory as follows

In Eq. 4.18 the expression given in brackets is a function of y and it is the effective angle of attack. The effective angle of attack is nothing but the difference between the sectional angle of attack a and the angle induced by the downwash which is also induced by the tip vortices of the wing.

An efficient method of solving Eq. 4.18 to find the spanwise circulation is the Glauert’s Fourier series method. Let us first transform the spanwise y and g coordinates from і to — і with

y = і cos / and g = і cos в

Expansion of the circulation distribution into sin series only enables us to have the vanishing circulation values at the tips. Having the Fourier coefficient with no dimension suggests the following form for the circulation expression

Г(ф) = Uaobo^^An sinn/. (4-19)

n=1

In Eq. 4.19 the coefficient aobo denotes the lift line slope and the half chord values at the root. Using 4.19 and its derivative in 4.18 we obtain

P

The integral tables give that / coc°/ПОСОО o

0 co co

Hence, we obtain

Equation 4.21 is valid for the whole span from left tip to right tip with An being the unknown coefficients once the geometry of the wing is specified. In order to determine these unknown coefficients we have to pick first N terms in the series together with the sufficient number of spanwise stations along the span so that we end up with the number of unknowns being equal to number of equations written for each station. After solving the system of equations for the unknown coeffi­cients, we obtain the circulation value at each station using 4.19. If we examine Eq. 4.19, we observe that for odd values of n, n = 1, 3, 5, … , the circulation values will be symmetric with respect to wing root and for even n, n = 2, 4, 6, ., will be antisymmetric. The integration of the circulation along the span with the Kutta-Joukowski theorem gives the total lift and the lift induced drag. For a symmetric but arbitrary wing loading the total lift and the induced drag coeffi­cients in terms of the aspect ratio AR and the wing area S become

CL = na0lb0lA1/S, (4.22a)

CDi = CL/(nAR)Y^ nA/A. (4.22b)

n=1

Prandtl’s lifting line theory helps us to find the pitching moment distribution along the span of a wing. At a section of a wing, the moment is determined as the summation of the moment acting at the center of pressure (mcp = 0) with the moment at the aerodynamic center (mac) where the moment is independent of angle of attack. Thus, we place the bound vortex at the quarter chord where the lifting force is acting. To find the moment at the quarter chord, the moment at the aerodynamic center is transferred to the quarter chord.

Shown in Fig. 4.2 is the line of centers of pressure and the line of aerodynamic centers for a swept wing which is symmetric with respect to its root. Let us first
find the distance XAC between the aerodynamic center of this wing to the reference line with integrating the sectional characteristics along the span

і

Cl(y)Xacb(y)dy

Xac = —l (4.23a)

Ci(y)b(y)dy

0

Now, the moment with respect to the aerodynamic center can be found with defining Dxac(y) = Xac – xac(y) at each section as follows

і

Mac = j (mac – L Axajdy (4.23b)

0

Here, L0 denotes the sectional lift.

Example 1: A rectangular wing which has an aspect ratio of 7 has a symmetrical profile. Find its lift coefficient in terms of the constant angle of attack a.

Solution: Since the wing is symmetric with respect to its root, we take only the value of odd n. It is sufficient to choose 4 station points with /, = p/8, p/4, 3p/8 and p/2 to find 4 unknown coefficients An, n = 1, 2, 3, 4 with four equations written for each station.

For a being constant at each station Eq. 4.21 gives

4

a,- = ^2 An sin n/i

n=1

Since the angle of attack is constant the solution of the final equation gives A1 = 0.9517a, A3 = 0.1247a, A5 = 0.0262a, A7 = 0.0047a The lift coefficient for the wing then becomes