Lighthill’s acoustic analogy

Lighthill’s acoustic analogy is a peculiar kind of object: it amounts to a model representation of the jet-noise problem, but one which is described by an exact fluid dynamics equation (nothing less than the Navier-Stokes equations is stated). This dual quality constitutes both the elegance of, and the crux of the interpretational difficulties associated with, the acoustic analogy formulations in general.

Lighthill sought to rearrange the equations of mass and momentum conservation—taken in their full, non-linear form—such that the wave op­erator would appear. In order to do so, he followed the same basic steps used in the derivation of the wave equation, but without performing the linearisation. Taking the time derivative of the mass conservation equation, the divergence of the momentum conservation equation, and combined the

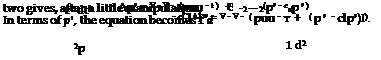These inhomogeneous wave equations can be interpreted in terms of a source term (the right hand side) that drives density or pressure fluctuations, as described by the left hand side.

We can now examine integral solutions to Lighthill’s equation, and it is at this point that we make a first connection between radiated sound energy and the flow characteristics of a turbulent jet.

These solutions can be considered on three levels: that of (1) elementary dimensional analysis; (2) time-averaged (second and higher order) statistics; and, (3) space-time analysis. The third of these gives us the most direct insight, in so far as it allows a local (in space and time) grasp of the sound production mechanisms; it is most useful for highly organised flows, and/or for understanding the organised component of high Reynolds number flows (‘coherent structures’). In the second approach, detailed understanding is hampered by time-averaging, and we are obliged to consider the connection between the radiated sound power and the jet flow via the second and higher order statistical moments of the unsteady flow; this kind of approach is most useful for the more random components of the flow unsteadiness. The first of the approaches is the most elementary of the three, where very little physical insight is provided regarding the underlying mechanisms. In section §3 we will revisit these representations when we discuss the role played by coherent structures in the generation of sound.

Integral solutions to equations 17 and 18 can be obtained using the Green’s function formalism outlined earlier. Henceforth we will change to tensor notation, we will only consider the equation expressed in terms of p’, and we will consider the simplified source quantity

the term associated with viscous effects t can be neglected for most flows of interest, and the third term on the right hand side of equation 18 is believed

3See Lighthill (1952) for full details.

to correspond to the effect of temperature fluctuations (this is often referred to as the entropy source term). This is probably an oversimplification, as in high Mach number flows there is evidence to suggest that the first and third terms on the right hand side of equation 18 are correlated (cf. Bodony and Lele (2005)). However, as our objective in this lecture is to make as clear as possible, and in as simple a manner as possible, the essential workings of acoustic analogies, we will continue to use this simplified scenario. Once the reasoning has been clearly understood in terms of the simplified source term, it is conceptually straightforward to extend to more complex source terms.

The free-field Green’s function is Go = ^—r, and so solution to

Lighthill’s equation can be written as follows:

From equation 20 we can proceed in two ways: (1) we can do the most basic kind of dimensional analysis, which will lead to the simplest expressions of the relationship between radiated sound power and flow characteristics; or, (2) we can take things from the statistical standpoint. We will here do both.

First, however, we introduce two simplifications that are frequently used. The first exploits the reciprocity property of the Green’s function, which means that source and observer can be interchanged. This allows the double divergence in equation 20, which is in terms of the source coordinates y, to be expressed in terms of the observer coordinates, x, at which point it can be taken outside the volume integral:

Now that differentiation is being performed in the observer frame (assumed to be in the farfield), where fluctuations are entirely acoustic, the spatial derivatives are related to temporal derivatives through

d xi 1 d

dxi x co dt ’

because we are dealing with a non-dispersive wavefield: if you want to know the spatial gradient of the waveform, rather than walk along the wave and measuring the slope as you go, you can simply stay put, letting the

XiXj d2 4nc2x3 dt2

wavefield pass you by, at the speed of sound; by then measuring its temporal rate of change, knowing it’s propagation speed and considering that the sound waves are locally plane, you immediately have access to the spatial derivative. The solution can thus be written, because we are in the farfield (Іж — y « |ж|), in the following simplified form:

Dimensional analysis Let us consider the problem of the subsonic propul­sive jet, which is the system that Lighthill’s analogy was first used to as­sess. If we consider that a characteristic eddy dimension in the turbulent jet plume is of the order of the jet diameter, D, which corresponds, ap­proximately, to the vorticity thickness of the mixing-layer at the end of the potential core of a subsonic jet[8], a characteristic frequency is f = Uo/D, where Uo is the exit velocity of the jet, and Df/co = Uo/co = M, where M is the Mach number (a measure of compressibility). This means that

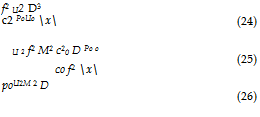p

I!2

and so the acoustic intensity, I = , should scale as

I =- pU3Ms(x) – U8. (27)

This very simple analysis immediately shows the very strong dependence of the sound power radiated on the velocity and Mach number of a jet. This was the first major result of Lighthill’s theory. In terms of jet noise control, if we are to judge an analysis in terms of the impact it has had on the design of the application, it remains the most significant result to date: it was clear from this analysis that the jet velocity and Mach number would need to be reduced, and that moderate reductions could lead to significant reductions
in sound power. In order to do so, without losing thrust, larger diameter jets would be required: the introduction, and subsequent optimisation of, the (low and high) by-pass jet engine led, between 1950 and 2000, to a 20dB reduction in the sound power radiated by jets exhausts at take-off.

16п2с0х[9] JV n Jv, dt2

d2UiUj ( t _ x – y’

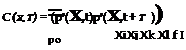Statistical analysis We now consider the second way in which it is pos­sible to relate radiated sound power to flow/source characteristics. Us­ing equation 23, expressions for the autocorrelation of the farfield pressure (which is related to the power spectrum of the pressure by a Fourier trans­form) can be obtained; this can then be related to the turbulence through the term puiUj. Assuming constant density in the source term (p = po), the autocorrelation function of the farfield pressure fluctuation is given by

^’t-‘^ + Ty^. (28)

And, if the turbulence is considered to be statistically stationary, the equa­tion can be rewritten as

n< ч xixjxkxi [ f d4 / ( , . x – y’ 15

C(x’t) = poйлухрА,,, V, дт-ЛщиАу •t -~^—>

Uk Ui( y” ,t-][X – y 1 + ^ ^dy’ dy". (29)

By virtue of this equation we now have a far more detailed description of how the sound power radiated by a jet flow is related to that flow: for a single observer in the farfield, at x, the sound power, as a function of frequency,[10] is given by a volume integral, over the entire extent of the jet, of the two-point, two-time correlation of the Reynolds stress field.

Instantaneous analysis The two approaches presented above, both of which involve considerable data compression when compared to the full space-time fields from which they begin (and where mechanisms show them­selves most exactly), necessarily hide a certain amount of information.6

Some kind of compression is of course indispensable: the formidable com­plexity of the full space-time structure of turbulence is such that useful assimilation and description is only possible at the expense of some such information loss. However, the ever-increasing capabilities of numerical simulation, experimental data acquisition and data post-processing, mean that new kinds of analysis and modelling methodologies, which deal more directly with the local space-time details of flow mechanisms, can be con­sidered. Such methodologies and tools, which are outline sections §3, §5 and §6, are essential from the point of view of real-time, closed-loop con­trol, towards which fluid dynamics research is headed. It is therefore useful to consider the space-time-local representation of the solution to Lighthill’s equation 20.

As outlined above, the physical system described by an inhomogeneous wave equation, such as Lighthill’s, involves a coupling between a source term—which in this sub-section we will simply refer to as q(x, t)—and some base-flow medium that can sustain propagative, wavelike perturbations in accordance with the balance expressed by the wave equation. In the context of Lighthill’s formulation, the mechanism by which a propagative wave is set up, in the quiescent medium, by the source, amounts to the acoustic matching described earlier. In order therefore to have access to what is happening in real time, we need to examine the integral solution in its most primitive form

What this equation tells us is that if we consider the excitation field in a distorted space-time reference frame, q(y, t — c y), the farfield pressure is given by simply summing all the points of that distorted field. If the source field is considered in undistorted space-time, additional time-delays, corresponding to wave-propagation times, weight the summation. Physi­cally, this summation corresponds to the time-delayed constructive and de­structive interference phenomena that underpin, respectively, loud or quiet source activity. We will discuss this in the next section when we consider the antenna-like wavepacket radiation associated with ‘coherent structures’.