. Precessional Stall Issues

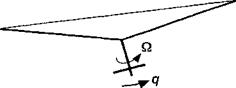
A problem that has occurred on tail rotors that can limit its thrust is a phenomenon known as precessional stall – see Lynn (1970). The tail rotor has no cyclic pitch and so it is free to flap in response to the changing aerodynamic forces. The tail rotor is subjected to higher effective angular rates than the main rotor as a result of yawing maneuvers, these rates being relatively large during turns about a point in hovering flight (so-called “spot – turns”). As described in Chapter 4, the rotor basically acts like a gyroscope so that when its shaft axis is suddenly tilted as the helicopter yaws the tail rotor initially maintains its orientation in inertial space – see Fig. 6.31. However, the tilting of the rotor shaft produces a change in blade pitch with respect to the original orientation of the tip-path-plane (TPP) and so a cyclic variation in blade lift is produced. This lift acts to create blade flapping and so begin to precess the rotor. The rotor plane, therefore, will align itself so that it once again becomes perpendicular to the rotor shaft. This realignment occurs rather quickly, certainly within one rotor revolution.

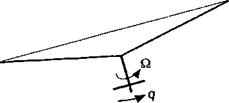
If the tail rotor shaft undergoes continuous angular displacements such as would be produced by the helicopter undergoing a yawing motion, the rotor disk will continuously try to realign itself. Because the realignment does not happen immediately, eventually the time rate of change of shaft displacement can become sufficiently high that the rotor TPP lags behind the shaft plane by a finite angle – see Fig. 6.32. The additional flapping moment on the blades resulting from gyroscopic effects on a rotor with pitch rate q and roll rate p is

Mg = —2Ib&q sin ф — 2h^p cos ф, (6.38)

(a) Where TPP actually is (b) Where TPP should be

Figure 6.32 A lag in tilt of the TPP is produced when the shaft is tilted at a finite rate.

which is derived in Gessow & Crim (1955) and Brown & Schmidt (1963). Solving the equation of motion for a flapping blade (Eq. 4.5) with these additional terms gives the flapping response of the rotor. For a combination of pitch rate q and roll rate p about the rotor у (lateral) and x (longitudinal) axes respectively, the lag in the blade flapping displacements (relative to where the TPP would be under steady conditions) are

which is for a rotor with no hinge offset, where у is the Lock number (see page 179) and д is the advance ratio of the rotor. It can be assumed for the tail rotor that a yaw rate Ф == q. This means that for a nose right yaw rate the tail rotor experiences an effective nose up pitch rate, causing a longitudinal lag in the blade flapping response combined with some smaller lateral flapping response.

The upshot is that when the angular rates (the yaw rate in this case) become sufficiently large, the blades will experience substantial changes in angles of attack that would be necessary to produce the aerodynamic forces to precess the tail rotor. For high enough rates, therefore, the flapping tail rotor blades will operate at such large angles of attack that they will approach stalled conditions. Because stall occurs as the tail rotor attempts to create aerodynamic forces to cause blade flapping and precess the orientation of the rotor plane, this phenomenon is called precessional stall. Precessional stall, therefore, can limit the anti-torque and directional (yaw) control of the tail rotor, and so can set a limit to overall helicopter performance. Lynn (1970) describe how this phenomenon may reduce attainable yaw rates. The situation is, of course, exacerbated when the helicopter is operating at high weights and/or high density altitudes whenever the tail rotor is operating under demanding thrust requirements and the blades are generating high lift coefficients.

In forward flight the tail rotor blades are already undergoing some flapping motion as a result of the dissymmetry in lift between the advancing and retreating sides of the disk. Therefore, by means of Eq. 6.39, it is apparent that relatively smaller angular yaw rates could produce precessional stall onset. Tail rotors typically have lower Lock numbers than the main rotor and, according to Eq. 6.39, the precessional effects will be relatively stronger, all other factors being equal. The onset of precessional stall can be reduced by using blades with increased Lock number (a byproduct of increased blade weight and flapping inertia) or by using rotor airfoils with larger C)max capability. Extra blade weight, however, is certainly not desirable and higher C/max is difficult to obtain without increasing torsional blade moments and control forces (see Section 7.7).