Pressure Correction for Extrapolation to Low-Speed Data

PSP is particularly effective in high subsonic, transonic and supersonic flow regimes. However, in low-speed flows where the Mach number is typically less than 0.3, PSP measurement is a challenging problem since a very small pressure change may not be sufficiently resolved by PSP. The major error sources, notably the temperature effect, image misalignment and CCD camera noise, must be minimized to obtain acceptable quantitative pressure results at low speeds. The resolution of PSP measurements is eventually limited by the photon shot noise of a CCD camera. Liu (2003) proposed a pressure-correction method as an alterative to extrapolate low-speed pressure data without directly attacking the intrinsic difficulty of PSP instrumentation for low-speed flows. This method is able to obtain the incompressible pressure coefficient from PSP measurements at suitably higher Mach numbers (typically Mach 0.3-0.6) by removing the compressibility effect.

It is noticed that there is a significant difference between the responses of the absolute pressure p and the pressure coefficient Cp to the freestream Mach

For Mі << 1, SC is much smaller than S„_p ; for Mf= 0.3 and

Cp p pf

dM f /M f = 10%, the relative change of the absolute pressure difference is d( p – pf )/(p – pf ) ~ 20% , while the relative change of Cp is only
dCp/Cp ~ 0.9%. Clearly, PSP can take the advantage of the relative insensitivity of Cp to the Mach number to obtain the approximate incompressible

pressure coefficient distribution at suitably higher Mach numbers. Furthermore, the compressibility effect can be corrected using the pressure-correction methods.

Historically, the pressure-correction formulas were derived in order to extrapolate the pressure coefficient in subsonic compressible flows from the incompressible flow theory and low-speed pressure measurements. In contrast, for PSP applications, the pressure-correction formulas are used to transform the compressible Cp to the corresponding incompressible Cpinc. The theoretical

foundation for pressure correction in 2D potential flows is well established. The linearized theory for subsonic compressible flows gives the Prandtl-Glauert rule (Anderson 1990)

Cp = Cpnc/Ji-мї. (5.38)

The use of a hodograph solution of the non-linear potential equation gives the Karman-Tsien rule (Anderson 1990)

C

Cp =———————– —p——————- T———– . (5.39)

For PSP measurements on 2D airfoils at suitably high Mach numbers, both the Prandtl-Glauert rule and Karman-Tsien rule can be used to recover the incompressible pressure coefficient. Bell and Hand (1998) used the Prandtl – Glauert rule for the purpose of improving the image ratioing procedure of PSP to obtain a pseudo wind-off pressure coefficient at a suitably low velocity. For complex 3D viscous flows such as separated flows, however, a general pressure – correction method is required.

Liu (2003) developed an iterative pressure-correction method for 3D flows. For Ml << 1, a pressure field can be generally expressed as a power series of Ml. The pressure-correction formula for a general surface Z = S( X, Y) has a functional form composed of an incompressible term and a compressible correction term

Cp « Cpinc + Ml F[X, Y,S( X, Y)] . (5.40)

Eq. (5.40) is valid for not only potential flows, but also complex viscous flows over a 3D body. Because Cpinc = Cpinc[ X, Y,S( X, Y)] is a function of X and Y,

we can, in principle, eliminate X in the correction function F[X, Y,S( X, Y)] by using Cpinc and Y. Therefore, since the correction function F[X, Y,S(X, Y)] is not specified yet, the equivalent form to Eq. (5.40) is

Cp « Cpnc + Ml F( CpinC, Y). (5.41)

Eq. (5.41) indicates that the pressure correction in 3D flows depends on not only Cpinc, but also one space coordinate Y. Note that the functional form of Eq. (5.41) remains valid after the coordinate Y is switched to another coordinate X. When

Cp does not change along the coordinate Y, Eq. (5.41) is naturally reduced to the method for 2D and axisymmetrical flows. By writing F(Cpinc, Y) as a polynomial function, Eq. (5.41) becomes

Cp « Cpinc + Mі £an(Y)Cliric. (5.42)

n=0

When the distributions of Cp and Cpinc are known along an intersection between the plane Y = const. and the surface Z = S( X, Y), the coefficients an(Y) can be determined using least-squares method. In wind tunnel measurements, pressure tap data in subsonic flow and the corresponding low-speed flow can be used to establish the relationship between Cp and Cpinc. However, this approach is not convenient for PSP measurements in wind tunnels since extra pressure tap data are required. Here, an iterative method is proposed to recover Cpinc from Cp data at

two different subsonic Mach numbers Mand Mi2. The biggest advantage of this method is that C inc can be directly obtained from two PSP images taken at

respectively, and assume M ^ < Mi2. Given the distributions of Cp1 and Cp2 along an intersection between the plane Y = const. and surface Z = S(X, Y), we need to solve the following equations to recover Cpinc and an(Y)

N

Cp1 « Cpinc + Mh Xan(Y)Cnpinc n=0

Cp2 ~ Cpinc + M22 Xan(Y)Cnpinc. (5.43)

n=0

An iteration scheme for solving Eq. (5.43) is described below.

(1) Give the initial distribution Cpinc(k) = Cp1 (k = 0) as a function of X along an

intersection between Y = const. and Z = S( X, Y) in the object space (a row or column in the image plane). Here, k is the iteration index number; (2) Determine the coefficients an(k)(Y) (n = 0,1…N) in the polynomial from a system of

N

equations (Cp2 – Cpinc(k))/M І2 = X an(k)(Y )C"pinc(k) using least-squares

n=0

N

method; (3) Substitute an(Y) into Cpinc(k+1) ~ Cp1 – Mh Xan(k)(Y )Cnpinc(k) to

n=0

obtain the corrected value Cpinc(k+1); (4) Go back to Step (2), replace Cpinc(k) by the corrected value Cpinc(k+1) and iterate until the converged results

Cpinc = Lim Cpinc(k) and an(Y) = Lim an(k)(Y) (n = 0,1…N) are obtained; (5)

Output the final Cpinc = Cpinc[X, Y,S(X, Y)] and an(Y).

After processing for a large set of intersections, we can recover the distribution of Cpinc on the whole surface. Unlike the classical pressure-correction formulas

for 2D flows, this iterative method is a non-local approach that has to be done along an intersection. The selection of the order N of the polynomial in Eq. (5.43) depends on the complexity of the Mach number effect on the pressure distribution along the intersection. For 2D flows and near-2D flows, N = 2 is sufficient; for more complex flows, the order of the polynomial could be higher. The number of available data points on an intersection eventually limits the order of the polynomial.

For PSP, data processing is typically done in the image plane rather than in the object space. Therefore, for convenience, the pressure-correction method should be used in the image plane. The aforementioned analysis is made in an arbitrary object-space coordinate system (X, Y,Z) or a general non-orthogonal curvilinear coordinate system on a surface. Since there is a one-to-one projection mapping between the image plane (x, y) and the surface Z = S(X, Y), the iterative pressure correction method can be directly applied to rows or columns in PSP images.

There are limitation conditions for application of the iterative pressure – correction method (actually for any pressure-correction method). First, the two

Mach numbers M x1 and M^2 should be lower than the critical Mach number at which flow becomes sonic at certain point on a surface. Secondly, the pressure – correction method relies on an assumption that the pressure distribution does not have a drastic change due to the Reynolds number effect as the Mach number increases from M ^ = 0 to M x1 and M ^2. When the Reynolds number effect on pressure overwhelms the effect of the Mach number, the pressure-correction method cannot produce correct results because the flow pattern has been qualitatively changed. This situation may happen on a high-lift model under certain testing conditions in certain flow separation regions that are particularly sensitive to the Reynolds number effect. Fortunately, there is a large class of flows in which the Reynolds number does not significantly affect the surface pressure distribution, such as attached flows and certain separated flows whose separation and re-attachment lines are fixed. For these flows, the pressure – correction method is applicable.

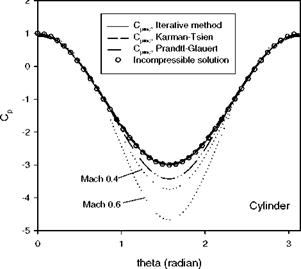
The iterative pressure-correction method was validated for flows over a circular cylinder, sphere, prolate spheroid, transonic body and delta wing (Liu 2003). Figure 5.16 shows the incompressible Cpinc distribution on a circular cylinder

recovered by the iterative pressure-correction method along with the results obtained using the Prandtl-Glauert rule and Karman-Tsien rule. The iterative method produced excellent recovery of Cpinc given by the incompressible solution

of potential flow over a cylinder (Lighthill 1954). The Karman-Tsien rule also gave a good correction while the Prandtl-Glauert rule was not accurate in the low – pressure region Cp = [ -3,-2 ] . The iterative method used the Cp distributions at Mx1 = 0.4 and M^2 = 0.6 . The order of polynomial was N = 2 and the solution for Cpinc converged after 10 iterations. Both the Karman-Tsien rule and Prandtl-

Glauert rule used Cp at M^ = 0.4 to recover Cpinc. Figure 5.17 shows the

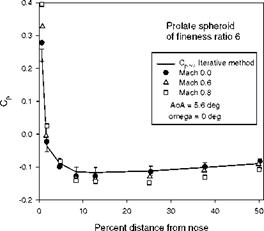
pressure correction for a prolate spheroid of a fineness ratio of 6 at the angle of attack of 5.6o and zero ellipsoidal coordinate (Matthews 1953). The iterative method used Cp data at Mx1 = 0.6 and Mx2 = 0.8. Even though these Mach

numbers are quite high, the iterative method still produced good results since the Mach numbers were less than the critical Mach number of 0.904 in this case. To examine the capability of the iterative pressure-correction method for complex vortical separated flows, it was also used to recover C inc on the upper surface of a 65o delta wing; the recovered Cpinc distributions showed a correct trend as the Mach number increases.

Fig. 5.16. Pressure correction for a circular cylinder to recover the incompressible pressure coefficient. From Liu (2003)

Fig. 5.17. Pressure correction for a prolate spheroid to recover the incompressible pressure coefficient. From Liu (2003)