QUASI-STEADY AERODYNAMIC DERIVATIVES
In an unsteady flow, the fundamental equation 2 of § 6.1 does not hold because y(x) now consists of both free and bound vortices. Moreover, since the lift, and hence the vorticity strength, varies with time, vortices
У
…. іепгпу w
<-
"h
c
Fig. 6.2. Unsteady flow over a two-dimensional airfoil.
must be shed at the trailing edge of the wing and carried downstream by the flow. The reason for this is that the total circulation in a contour enclosing all the singularities (Fig. 6.2) must remain zero in a nonviscous fluid. Therefore every vortex element on the wing must be balanced by another in the wake. The vortices in the wake, having no force to support
them, cannot have relative velocity with the flow and hence move downstream along the streamlines. These wake vortices, however, induce vertical components of velocity on the wing, and therefore the second fundamental equation (Eq. 4 of § 6.1) also becomes invalid.
In order to make a simplified analysis, let us introduce the following quasi-steady assumption: The aerodynamic characteristics of an airfoil whose motion consists of variable linear and angular motions are equal, at any instant of time, to the characteristics of the same airfoil moving with constant linear and angular velocities equal to the actual instantaneous values. The inclination of the flow-velocity vector to the profile is also taken to be constant and equal to the actual instantaneous inclinations. Thus, at any instant of time, we assume that Eqs. 2 and 4 of § 6.1 hold, in spite of the objections named above.
Under the quasi-steady assumption, the results of the last section can be applied directly. Let us consider a flat plate in a stream whose velocity at infinity is U in the ж-axis direction. Let the plate have two degrees of freedom: a vertical translation h and a rotation a about an axis located at x0 behind the leading edge, h being positive downward and a positive nose up, both measured from the ж axis. Let the coordinate system be as shown in Fig. 6.2. As before, the plate will be replaced by a vortex sheet, and the camber line, when h — a. = 0, is a line Y(x) = 0.
At a point ж on the airfoil, the vertical velocity component is
The instantaneous slope of the airfoil at ж is ■— a. As the fluid velocity must be tangential to the airfoil, the vertical component of fluid velocity V{ on the airfoil must satisfy the equation
v{ is the velocity induced by the vorticity yfr). Equation 1 is the equivalent to Eq. 5 of § 6.1. A comparison with the fundamental equations of § 6.1 shows that everything is the same except that the term dY/dx in that section must now be replaced by
![]() (ж0 — ж) da – —
(ж0 — ж) da – —
Making this replacement in Eqs. 15 of § 6.1, we obtain, from Eqs. 16 and 14 of §6.1
![]() ^ dCj, J 1 dh 1 /3 da
^ dCj, J 1 dh 1 /3 da
Should хл and U be zero, Eqs. 3 would be reduced to two independent equations, one for h and one for я. The terms involving xx and U indicate inertia and aerodynamic couplings.
Since Eqs. 3 are linear equations with constant coefficients, the solution is a sum of linearly independent solutions of the form
h = Af(y)eu, a. = В ф(у)еи (5)
where Я,/(у), ф(у) and А, В are to be determined from Eqs. 3 and 4, and the initial conditions. Since the solution of a differential equation depends continuously on the coefficients of the equation, and since the coefficients of Eq. 3 vary continuously with U, the constant Я will vary continuously with U. In general, Я is a complex number. Let
Я = p + щ (6)
When p is positive, the amplitude of the motion will increase with increasing time. When p is negative, the opposite is true. If p is negative at иъ and positive at U2, (U2> U{), then there exists at least one value of U, say U0, between U1 and U2, at which p vanishes. At U0, p is purely imaginary, corresponding physically to a simple-harmonic motion. Such a speed will separate the speed range in its neighborhood into two regions, in one of which p < 0, where the motion is damped and stable; in the other p > 0, where the amplitude increases with time and is unstable.
Beginning with U = 0, let us gradually increase the speed of flow and consider the variation of p with U. When U = 0, the motion is simple
harmonic, and so p = 0, as is shown in § 1.10 (material and air damping neglected). Next let U be a very small positive number. We shall show that p is small and negative. Instead of solving the differential system directly, let us recall that p < 0 implies that the motion is damped. For a free system this imples that the wing is losing energy to the surrounding air. Hence, it is sufficient to consider the energy relations. When U is small, the solutions h and oc differ only slightly from those obtained for U — 0. Free oscillation in still air has been investigated in § 1.10, where it is shown that the solution can be written as
h — A fly) sin qt, а — В ф(у) sin qt (7)
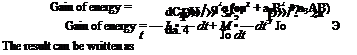 |
|
where A, B, q are real numbers and f ф are real functions, h and a are in phase with each other, so the initial phase angles may be omitted from Eqs. 7 by suitably choosing the origin of time. The oscillation modes h and a at very small V will be assumed to be given by Eqs. 7. Substituting Eqs. 7 into Eqs. 2 to obtain L and M, we can compute the energy gain per unit span of the wing at a spanwise station у in each complete cycle of oscillation:
where
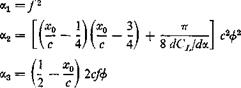 (10)
(10)
Evidently ax > 0. a2 reaches a minimum at xfc — x/2 where it becomes zero if dCJda — 2тг, and is positive if dCL/da < 2tt. Furthermore, if dCjjda < 2tt, the discriminant of Eq. 9 is negative; i. e.,
у – axa2 <0 (11)
For we may reduce the discriminant into the following form:
![]()
 /У-2 / 277 C2/2<P
/У-2 / 277 C2/2<P
dCjda) 16
which is zero when dCL/da = 2n and is negative when dCLjda < 2n. Therefore the quadratic form of A and В in the parenthesis of Eq. 9 is
nonnegative,* and Eq. 9 shows that the airfoil cannot gain energy from the flow. In other words, when the speed of flow U is infinitesimal, the flow is stable and p is negative. f Since p = 0 when U = 0, it is evident that p will remain negative until it becomes zero again at certain higher value of U, say Ua (see Fig. 6.4). For speeds U > UCI> p may become positive, corresponding to an unstable motion.
We shall call the speed at which p — 0 a critical speed. We have shown that between U = 0 and U„ the torsion-flexure motion of the cantilever wing is stable when dCLjda. < 277. At the critical speed, two cases are possible: Either q (the imaginary part of A) vanishes, or it does not vanish.
|
|
If q — 0, then the displacements h and a are independent of time, but the structure has lost its power to recover its original form when disturbed. The wing is said to be in critical divergent condition. If q Ф 0, the motion is harmonic with an indefinite amplitude. It is said to be in the critical flutter condition. Hence,
p = 0, q — 0 implies divergence p — 0, q Ф 0 implies flutter
In both cases the aeroelastic system may be said to be neutrally stable.
The continuity argument cannot establish definitely the sign of p for U > C/cr. As shown in Fig. 6.4, at UCT there are two possibilities. The curve of p vs. U may cross the U axis to p > 0 for U > UCI (curve a), or it may have a horizontal tangent at f/cr and then turn back to the lower side (curve b). More careful study in the neighborhood of UCI is necessary
* A quadratic form ax2 + bxy + су2 can never change its sign for all real values of (ж, у), if
b2 — 4ac < 0
t This result has no universal validity since the case xjc = 1/2, dCflda = 2-n must be excepted. Nor is it true for all other types of oscillations. For example, in tab flutter problems, it may happen that a disturbed motion is actually unstable for zero airspeed upwards for bad values of tab frequency and mass balance. In general, a test of stability is needed. Such a test will be discussed in § 6.5 and in § 10.6.
to establish the tendency definitely. In practice, the first case is what generally occurs: The motion at supercritical speeds is unstable.
When we continue curve a or b further for larger values of U, it may cross the U axis again. Hence, higher critical speeds may exist. But, since aircraft flight starts from U = 0 and increases continuously, and since generally no instability can be tolerated, the flight speed cannot be permitted to be larger than the first critical value. Thus the finding of the first critical speed is the main object of flutter analysis.
That only the critical speed is of interest implies the following important facts:
1. Only undamped harmonic oscillations are of interest. Hence the aerodynamic coefficients need only be evaluated for harmonic motions.
2. At the critical condition, the amplitude of oscillation may be considered as infinitesimal. There is no need to discuss finite deformations. The linearized aerodynamical theory and the linearized equations in elasticity can thus be justified in most cases.












