Special cases of the BiotSavart law

Equation (5.6) needs further treatment before it yields working equations. This treatment, of integration, varies with the length and shape of the finite vortex being studied. The vortices of immediate interest are all assumed to be straight lines, so no shape complexity arises. They will vary only in their overall length.

A linear vortex of finite length AB Figure 5.10 shows a length AB of vortex with an adjacent point P located by the angular displacements a and /? from A and В respectively. Point P has, further, coordinates r and 6 with respect to any elemental length 8s of the length AB that may be defined as a distance s from the foot of the perpendicular h. From Eqn (5.7) the velocity at P induced by the elemental length 8s is

in the sense shown, i. e. normal to the plane APB.

To find the velocity at P due to the length AB the sum of induced velocities due to all such elements is required. Before integrating, however, all the variables must be quoted in terms of a single variable. A convenient variable is ф (see Fig. 5.10) and the limits of the integration are

<74 =-(I-a) to <6B = +(|-/?)

since ф passes through zero when integrating from A to B.

sin в = cos ф, r2 = h2 sec2 ф dr = d(h tan ф) = h sec2 фд. ф

The integration of Eqn (5.8) is thus

,+(*/2-/3) Г Г Г. /7Г N. /7Г ] = —-гсозфаф = —— sin — р + sin — а J-M2-а) 4тгй v y 4тгА L V2 и) 2 )

р+(тг/2-/3) p -(*/2-a)

Г, „

– —— (cos а + cos в) 4тгп ‘

This result is of the utmost importance in what follows and is so often required that it is best committed to memory. All the values for induced velocity now to be used in this chapter are derived from this Eqn (5.9), that is limited to a straight line vortex of length AB.

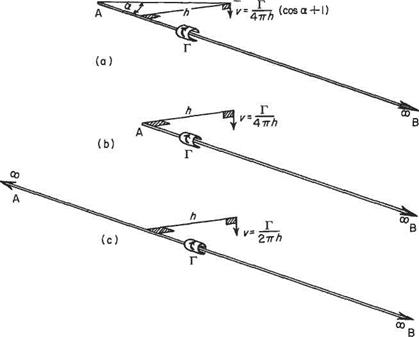
The influence of a semi-infinite vortex (Fig. 5.11a) If one end of the vortex stretches to infinity, e. g. end B, then /3 = 0 and cos /3 = 1, so that Eqn (5.9) becomes

Г,

v = —* (cos a + 1) 47ГЙ

When the point P is opposite the end of the vortex (Fig. 5.11b), so that a = 7t/2, cos a = 0, Eqn (5.9) becomes

The influence of an infinite vortex (Fig. 5.11c) When a = /3 = 0, Eqn (5.9) gives

Г

2nh

and this will be recognized as the familiar expression for velocity due to the line vortex of Section 3.3.2. Note that this is twice the velocity induced by a semi-infinite vortex, a result that can be seen intuitively.

In nature, a vortex is a core of fluid rotating as though it were solid, and around which air flows in concentric circles. The vorticity associated with the vortex is confined to its core, so although an element of outside air is flowing in circles the element itself does not rotate. This is not easy to visualize, but a good analogy is with a car on a fairground big wheel. Although the car circulates round the axis of the wheel, the car does not rotate about its own axis. The top of the car is always at the top and the passengers are never upside down. The elements of air in the flow outside a vortex core behave in a very similar way.

P

Fig. 5.11