The Biot-Savart law

The original application of this law was in electromagnetism, where it relates the intensity of the magnetic field in the vicinity of a conductor carrying an electric current to the magnitude of the current. In the present application velocity and vortex strength (circulation) are analogous to the magnetic field strength and electric current respectively, and a vortex filament replaces the electrical conductor. Thus the Biot-Savart law can also be interpreted as the relationship between the velocity induced by a vortex tube and the strength (circulation) of the vortex tube. Only the fluid motion aspects will be further pursued here, except to remark that the term induced velocity, used to describe the velocity generated at a distance by the vortex tube, was borrowed from electromagnetism.

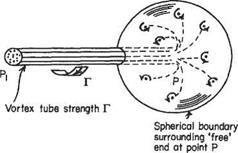
Allow a vortex tube of strength Г, consisting of an infinite number of vortex filaments, to terminate in some point P. The total strength of the vortex filaments will be spread over the surface of a spherical boundary of radius R (Fig. 5.7) as the filaments diverge from the point P in all directions. The vorticity in the spherical surface will thus have the total strength Г.

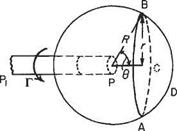
Owing to symmetry the velocity of flow in the surface of the sphere will be tangential to the circular line of intersection of the sphere with a plane normal to the axis of the vortex. Moreover, the direction wifi be in the sense of the circulation about the vortex. Figure 5.8 shows such a circle ABC of radius r subtending a conical angle of 29 at P. If the velocity on the sphere at R, 9 from P is v, then the circulation round the circuit ABC is Г’ where

r/ = 27ri? sin0v (5.1)

Fig. 5.8

Putting r = radius of circuit = R sin 0, Eqn (5.1) becomes

Г’ = 2ttrv (5.2)

Now the circulation round the circuit is equal to the strength of the vorticity in the contained area. This is on the cap ABCD of the sphere. Since the distribution of the vorticity is constant over the surface

p, _ surface area of cap ^ _ 2тгі?2(1 — cos 0) surface area of sphere 4тгR2

Equating (5.2) and (5.3) gives

Now let the length, PP, of the vortex decrease until it is very short (Fig. 5.9). The circle ABC is now influenced by the opposite end P. Working through Eqns (5.1),

(5.2) and (5.3) shows that the induced velocity due to Pi is now

Vl = 4^(1_ cosffl)

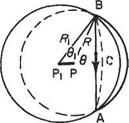since r = Ri sin 0i and the sign of the vorticity is reversed on the sphere of radius R as the vortex elements are now entering the sphere to congregate on Pi.

The net velocity in the circuit ABC is the sum of Eqns (5.4) and (5.5):

Г

V — Vi = ——————— [1 — COS 6 — (1 – COS#])]

47Г r

— (cos 6 — cos 6)

47ГГ

As Pi approaches P

cos 6 —► cos(0 — 86) = cos 6 + sin 6 86

and

V — Vi

giving

8v = -—sn686
47ГГ

This is the induced velocity at a point in the field of an elementary length 8s of vortex of strength Г that subtends an angle 86 at P located by the coordinates R, 6 from the element. Since r = і? sin# and R86 = fosin# it is more usefully quoted as: