Aerodynamic characteristics for symmetrical general loading

The operations to obtain lift, downwash and drag vary only in detail from the previous cases.

Lift on the wing

and changing the variable z = — s cos в,

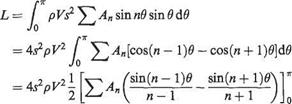and substituting for the general series expression

The sum within the squared bracket equals zero for all values of n other than unity when it becomes

Thus

L = Anr^pV^s2 = Cj}-pV2S

and writing aspect ratio (AR) = As^jS gives

Cl = ttAi(AR) (5.47)

This indicates the rather surprising result that the lift depends on the magnitude of the coefficient of the first term only, no matter how many more may be present in the series describing the distribution. This is because the terms AzsinW, As sin 50, etc., provide positive lift on some sections and negative lift on others so that the overall effect of these is zero. These terms provide the characteristic variations in the spanwise distribution but do not affect the total lift of the whole which is determined solely from the amplitude of the first harmonic. Thus

CL = тг(АЛ)Аі and L = 2тгpV4Ax (5.47a)

Down wash

Changing the variable and limits of Eqn (5.32), the equation for the downwash is

cos в — COS 6

In this case Г = 4sV£A„ sinпв and thus on differentiating

dr

— = 4sV Y’ nA„ cos пв d в "

Introducing this into the integral expression gives

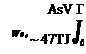
As V nA„ cos«0

COS в — COS Oi

= — y^nA„G„

7Г

and writing in G„ = 7rsinn0i/sin0i from Appendix 3, and reverting back to the general point в:

This involves all the coefficients of the series, and will be symmetrically distributed about the centre line for odd harmonics.

Induced drag (vortex drag)

The drag grading is given by dv = pwT. Integrating gives the total induced drag

pwTdz

or in the polar variable

This can be demonstrated by multiplying out the first three (say) odd harmonics, thus:

1= [ (A sin0 + ЗЛ3 sin30 + 5Л5 sin50)(.4i sin0 + A3 sin30 + As sin0)d0 Jo

= I {A sin2 0 + ЗЛ2 sin2 0 + 5A2 sin2 0 + [A 1A3 sin 0 sin 30 and Jo

other like terms which are products of different multiples of 0]} d0

On carrying out the integration from 0 to 7г all terms other than the squared terms vanish leaving

I = J (A2 sin2 0 + ЗЛ2 sin2 30 + SA sin2 50 H – )d0

= 2 f-4? + 3A + 5As ■!—- ] =

This gives

From Eqn (5.47)

cl

7Г2{ARf

C*=^(AR)[l+Sl

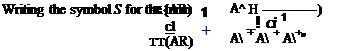and introducing this into Eqn (5.49)

Plainly 6 is always a positive quantity because it consists of squared terms that must always be positive. Cp, can be a minimum only when <5 = 0. That is when A3 = As = Aj = … = 0 and the only term remaining in the series is A sin 9.