Aerodynamic Design of a Rotor Blade—Betz Minimum Energy Condition

10.4.1 Formulation

The minimum energy condition of Betz [8] refers to the optimum conditions which lead to the minimum loss of energy in the slipstream. It applies equally to propellers and wind turbines. For the latter, the optimum distribution of circulation Г(y ) min­imizes the torque (negative) for a given thrust on the tower. The simple argument of Betz is that, in this case, an elementary force 8CT = —Г(y) (at – + w(y) dy should produce a constant elementary torque 8CT = ПГ(у) (1 + u(y)) ydy, inde­pendent of y. Hence the minimum energy condition of Betz reads

(1 + u (y)) y

y = y tanФ(у) = const. (10.43)

adv + w(y)

This is true only for vanishing circulation and induced velocities, as will be shown later. By analogy, lets consider the problem of the optimum wing loading in the Prandtl lifting line theory. Given that the lift and induced drag are

where w(y) is the downwash (negative),

Munk [9] showed that, for the optimum loading, the downwash w has to be constant, else, moving a small element of lift (elementary horseshoe vortex) 8CL = 28Гdy from its current position yi to a position y2 such that 8w = w(y2) — w(y) > 0, would not change the total lift, yet would change the induced drag by 8CDt = —28Г8wdy < 0, a decrease in total drag, indicating that the distribution is not optimal. In other words, for an elementary 8CL = 2Гdy, the induced drag 8CDt = —2Г(у^(у^у should be independent of y, which implies that w(y) = const. A more mathematical proof consists in considering the objective function

F (Г) = Cot (Г) + XCl (Г) (10.46)

consisting of the induced drag to be minimized for a given lift, where X is the Lagrange multiplier. Taking the Frechet derivative yields the minimization equation that must hold for any change 8Г of circulation. The Frechet derivative can be defined as the limiting process

d F d

(8 Г) = lim F (Г + в8Г)

д Г( ) в^0 d0y 2

The result is linear in 8 Г. It represents the derivative of F with respect to Г, in the direction of 8Г. Here we obtain:

d F l’1 ( dw l’1

— (8Г) = – 8^y)w(y) + Г(y) — (8Г) dy+2Xj 8Г(у)<іу (10.48)

But the kernel of w(Г) is antisymmetric. Hence, integration by part twice using the fact that Г(±1) = 8 Г(±1) = 0, yields the identity

dw

Г( y) (8 Г) = 8Г w( Г) d Г

Indeed, consider the second term in the integral above. By definition of the Frechet derivative of w(Г) in the direction 8 Г

f1 dw f1 1 f1 8 Г'(Ш n

L Г( y)-(8 ndy = Г( y){ – -1 –Л )

I = _1 Ґ Ґ Г(y)8Г’Шndy 4n -1 -1 y – n

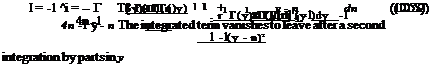A first integration by parts in n yields

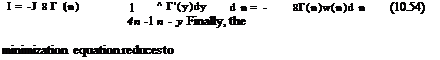Again the integrated term vanishes and the second term, thanks to the antisym­metry of the kernel y-y, can be interpreted as

d F f1

— (8Г) = -2j 8Г(y) (w(y) – X) dy, V8Г

The solution is simply w(y) = A. = const., as obtained by Munk with his simpler argument. The antisymmetry of the kernel simply indicates that two elementary horseshoe vortices of same intensity placed at y1 and y2 induce downwash that are opposite at the other horseshoe location. This is not the case with a wind turbine wake, because two vortices along the helix will have different shapes depending on their initial y-location at the blade, hence induce velocities u or w are not related. Let yv, zv be the equation of the vortex sheet of blade 1

yv = n cos( adkx))

zv = n sin(шїщ)

A vortex filament corresponds to a fixed value of n. Two such vortices are shown in Fig. 10.10.

The kernel for u and w does not have the antisymmetry property for the helicoidal vortex sheet as can be seen from the formulae

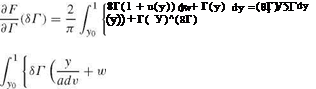stating that the search is for minimum torque (negative) for a given thrust on the tower at a given tip speed ratio and blade root location y0. The minimization equation is derived for one blade as

The terms such as Г(у)дГ (&Г) cannot be transformed in this case, however, choosing 8Г = Г yields the following identity

J Г {(1 + 2u(y)) у – л(ayv + 2w(y^} dy = 0 (10.61)

y

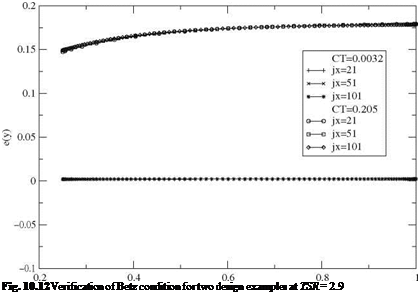
the interpretation of which is that the optimum solution satisfies the minimum energy condition of Betz, in the Trefftz plane, “in the average”, with Г as weighting factor. For a tip speed ratio TSR = 2.9, the design of a two bladed-rotor at (Cl )opt = 0.8979 with very light loading demonstrates that the minimum energy condition of Betz is verified. The thrust coefficient is CT = 0.0032, the corresponding value of the Lagrange multiplier is X = 0.3433 and the power coefficient Cp = 0.0031. For a higher loading, corresponding to the two-bladed NREL rotor at the same TSR and CT = 0.205, one finds X = 0.254 and Cp = 0.1768. The deviation from the Betz condition, e(y) = (y tan ф(у) – X)/X, is shown in Fig. 10.12. As can be seen, for lightly loaded rotor, the Betz condition is satisfied, but it is no longer the case when loading is more realistic.