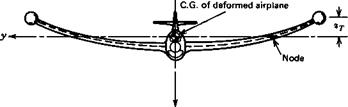
Aeroelastic Derivatives
In Sec. 4.12 there were introduced aerodynamic derivatives associated with the deformations of the airplane. These are of two kinds: those that appear in the rigid-body equations and those that appear in the added equations of the elastic degrees of freedom. These are illustrated in this section by consideration of the hypothetical vibration mode shown in Fig. 5.17. In this mode it is assumed that the fuselage and tail are rigid, and have a motion of vertical translation only. The flexibility is all in the wing, and it bends without twisting. The functions describing the mode (4.11,1) are therefore:
jc’ = 0
У’ = 0 (5.10,1)
z’ = h(y)zT
For the generalized coordinate, we have used the wing-tip deflection zT. h(y) is then a normalized function describing the wing bending mode.
Since the elastic degrees of freedom are only important in relation to stability and control when their frequencies are relatively low, approaching those of the rigid – body modes, then it is reasonable to use the same approximation for the aerodynamic forces as is used in calculating stability derivatives. That is, if quasisteady flow theory is adequate for the aerodynamic forces associated with the rigid-body motions, then we may use the same theory for the elastic motions.
|
Figure 5.17 Symmetrical wing bending. |
In the example chosen, we assume that the only significant forces are those on the wing and tail, and that these are to be computed from quasisteady flow theory. In the light of these assumptions, some of the representative derivatives of both types are discussed below. As a preliminary, the forces induced on the wing and tail by the elastic motion are treated first.