Berechnung des Gesamtauftriebes

Der Gesamtauftrieb eines Tragfliigels endhcher Spannweite er – gibt sich nach Gl. (5.42) durch Integration der Auftriebsverteilung und nach Gl. (7.7) durch Integration der Zirkulationsverteilung Г(у) iiber die Fliigelspannweite zu:

A = їоо/ca(y) l(y) dy = qU^JГ(у) dy. (7.59)

— S —S

Dabei bedeutet die Anstromgeschwindigkeit des Fliigels, = = q den Staudruck und ca(y) den ortlichen Auftriebsbeiwert des

Fliigelschnittes y. Wahrend die erste Beziehung nach den Gin. (7.42) und (7.43) durch Integration der Druckverteilung iiber die Fliigelflache

gewonnen wird, folgt die zweite Beziehung aus dem Kutta-Joukowsky- schen Satz.

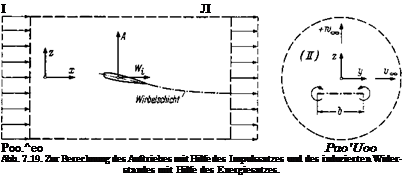Nachstehend soil eine weitere Beziehung fur den Gesamtauftrieb durch Anwendung des Impulssatzes abgeleitet werden. Nach Abb. 7.19

wird eine zylindrische Kontrollflache um den Tragfliigel gelegt. Die Achse des Zylinders verlauft in der Richtung der Anstromungsgeschwindigkeit U00. Die beiden Grundflachen I und II der zylindrischen Kontrollflache sollen sich sehr weit vor bzw. sehr weit hinter dem Fliigel befinden. Der Durchmesser des Kontrollzylinders wird so groB gewahlt, daB auf der Mantelflache Druck und Geschwindigkeit die Werte p^ bzw. Uqq der ungestorten Stromung haben wie auf der Flache I. Falls man nur den Auftrieb mittels des Impulssatzes berechnen will, kann man naherungsweise annehmen, daB die freie Wirbelschicht sehr weit hinter dem Fliigel zur Anstromrichtung parallel ist.1

Die durch ein Flachenelement dy dz der Flache II pro Zeiteinheit hindurchtretende Fliissigkeitsmasse betragt qU^dydz. Sie liefert zu – sammen mit der vom Fliigel induzierten Geschwindigkeit eine Impulskomponente in z-Richtung von der GroBe qTJ00w00dy dz. Da auf der Flache I die induzierte Geschwindigkeit Null ist, stellt das Integral dieses Impulses iiber die Flache II die senkrecht zur Anstrom­richtung auf den Tragfliigel ausgeiibte Kraft, d. h. den Auftrieb, dar:

A = —qU^ JJ wxdy dz. (7.60)

(ii)

Diese Beziehung gilt sowohl fiir die nicht aufgerollte als auch fur die aufgerollte Wirbelflache hinter dem Fliigel, vgl. W. Kaufmann [35].

1 Auf die entscheidende Bedeutung der Neigung der Wirbelflache bei der Be­rechnung des induzierten Widerstandes mittels des Impulssatzes hat K. Kraemer [39] hingewiesen, vgl. auch [79].

Im folgenden moge fur die nichtaufgerollte Wirbelflache die Gleich – wertigkeit der Gl. (7.60) mit der zweiten Beziehung in Gl. (7.59) gezeigt werden. Das Feld der induzierten Geschwindigkeiten sehr weit hinter dem Fliigel laBt sich mit Hilfe eines zweidimensionalen Geschwindigkeits – potentials Ф(у, z) darstellen, vgl. Gl. (7.55a), wobei

дФ

=——

00 dz

ist. Setzt man diesen Ausdruck in Gl. (7.60) ein, so wird nach Aus- fiihrung der Integration iiber z:

+ oo

a = – qvx i [<pi:_^dy.

y=- oo

An den Grenzen у — Az00 und z — ±00 verschwinden die Werte Ф, wahrend in der Wirbelflache, bei z = ±0, das Potential in z-Richtung einen Sprung vom Betrage АФ(у, 0) = Ф0(у, 0) — Фи (у, 0) hat. Mithin wird

A = gU0Of ЛФ(у, 0)dy.

Dabei konnten die Integrationsgrenzen у — ±00 durch у = A-s — Azb/2 ersetzt werden, weil auBerhalb der Fliigelspannweite АФ(у, 0) = 0 ist. Innerhalb der Fliigelspannweite ist, wie in Gl. (7.52b) gezeigt wurde, der Potentialsprung АФ gleich der Zirkulation Г(у). Damit ergibt sich in Ubereinstimmung mit Gl. (7.59):

A — Q Vao j Г(у) dy. (7.61)

— s

Der Gesamtauftrieb eines Fliigels hangt also nur von der Zirkulations – verteilung langs Spannweite des Fliigels ab. Dabei ist es gleichgiiltig, ob die Zirkulationsverteilung durch die FliigelgrundriBform (Seitenverhalt – nis, Pfeilung, Zuspitzung), durch eine Fliigelverwindung oder durch die Wolbung der Fliigelflache erzeugt wird.

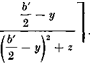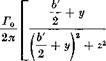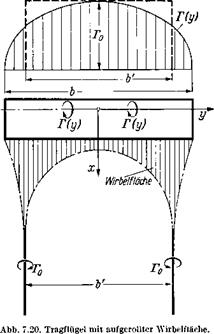
NaturgemaB gilt Gl. (7.60) auch fiir die aufgerollte Wirbelflache. Es sei nach Abb. 7.20 fiir eine symmetrische Zirkulationsverteilung langs Spannweite nun V der Abstand der beiden freien Wirbel mit der Zirku – lationsstarke Г0. Fiir die induzierte Geschwindigkeit in einem Punkt y, z der Querebene sehr weit hinter dem Fliigel (x 00) ergibt sich nach dem Biot-Savartschen Gesetz:

Setzt man diesen Ausdruck in Gl. (7.60) ein, so erhalt man nach sorg – faltiger Ausfiihrung der zweifachen Integration:

A — q U^r^b’. (7.62)

Unter Beriicksichtigung des Kutta-Joukowskyschen Auftriebssatzes sagt diese Formel aus, daB der Auftrieb eines Fliigels der Spannweite

b = 2s mit der veranderlichen Zirkulationsverteilung Г(у) gleich ist dem Auftrieb eines Fliigels der Spannweite V mit liber der Spannweite konstanter Zirkulationsverteilung Г0.

Durch Vergleich von Gl. (7.61) mit (7.62) ergibt sich fur den Abstand der beiden freien Wirbel:

6/2

b’=jrjr(y)dy. (7.63)

0

Diese Beziehung laBt sich auch so deuten, daB beim Aufrollen der Wirbelflache das Wirbelmoment um die Langsachse (a;-Achse) konstant

bleibt. Fur die rechte Fliigelhalfte ist das Moment der nicht aufgerollten

6/2

/

dr

— у dy und dasjenige der auf-

dy

gerollten Wirbelflaehe gleich Г0Ь’/2. Setzt man beide Ausdriicke gleich und fiihrt man bei dem Integral noch eine partielle Integration aus, dann findet man sofort die Beziehung (7.63). Zahlenwerte von b’/b werden in Abb. 11.18 mitgeteilt.