EQUATIONS OF MOTION OF A TWO-DIMENSIONAL AIRFOIL

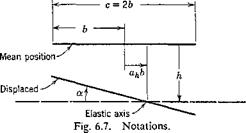Let us consider a strip of unit width of a two-dimensional flat-plate airfoil having two degrees of freedom: a bending h (positive downward measured at the elastic axis) and a pitching a (positive nose-up) about the

elastic axis (Fig. 6.7). Let the airfoil be situated in a flow of an incom­pressible fluid at speed U. The equations of motion of the airfoil will be derived by considering the balance of the inertia, elastic, aerodynamic, and exciting forces.

For an element of mass dm situated at a distance r (positive toward the trailing edge) from the elastic axis, the inertia force is

— dm(h + r’d)

* It is interesting to note that, whereas the apparent mass of a flat plate is equal to the mass of a cylinder of air with diameter equal to the chord of the plate, the apparent moment of inertia is only one fourth of the mass moment of inertia of that cylinder of air if that cylinder were solid.

The total inertia force per unit span of the wing is therefore

— J dm(h + r’d) = — (mh + S&) (1)

where m — dm = the total mass of the wing per unit span, slugs, and S = Jr dm = wing static moment about the elastic axis, slug-feet. The integrals are taken over the entire wing chord.

The inertia force exerts a moment per unit span about the elastic axis of amount

— j>(/i + rx)dm = — {LjV – + Sh) (2)

where Ix = r2dm = wing mass moment of inertia about the elastic axis, slug-ft2.

Let the bending and pitching displacements be resisted by a pair of springs at the elastic axis with spring constants Kh (pounds per foot) and Kx (foot-pounds per radian), respectively. The elastic restoring force corresponding to a displacement his — h Kh, in the direction opposing h. That against a is — aKx.

The equations of motion can be written according to the condition that the sum of the inertia and elastic forces and moments must balance the externally applied force and moment. Let the latter be denoted by Qh and Qx, which include the aerodynamic forces and other mechanical excitations. Hence,

mh + Sol + hKh = Qh, Sh + Ia к + — Qx (3)

These equations can be written in a slightly different way by expressing the spring constants in terms of certain frequencies. Consider the airfoil to be so restrained that only one degree of freedom, say h, is permitted. Assume further that no external force is acting. The equation of motion of the airfoil is then

mh + hKh =0 (a = 0) (4)

This represents an independent (uncoupled) harmonic oscillation of frequency

KJm (5)

Hence, we may write

Kh = mcoh2 (6)

Similarly,

Ka = W (7)

where a>x (radians per second) is the uncoupled natural frequency in torsion.

The part of the external forces induced by the motion of the airfoil can
be obtained from the results of the preceding section. The aerodynamic lift and moment about the elastic axis induced by h and a are:

L(t) = 2-rrbpU2j J>(t — г,,) |а'(т0) + h"(r0)

+ Q — ah) а"(то)] dr0 + pirUh" — афа!’) + pnbU4′

M(T) ^ (2 + ahj 2TTb2pUsj Ф(r — r0) Ci'(r0) + j – h"(r0)

+ ~ a*) a"(To)] *0 + ahbpnU2(h” – афа.")

If we let P(t) and Q(r) denote, respectively, the external applied force (positive downward) and moment (positive nose up) other than the aerodynamic lift and moment, and introduce the dimensionless time t = Ut/b, Eqs. 3 become*

w — /z" + $ — a" + mm^h — — Цт) + P(r)

U2 U2

Я – p – A" + /« a" + /a«a2« = M(r) + G(t)

Equations 10 can be solved by the method of Laplace transformation. But a special case is of interest: the steady-state forced oscillation due to a periodic excitation, in which the integrals in Eqs. 9 can be integrated explicitly, thus simplifying the calculations.