Flow Below the Lifting System and Its Wake (Channel Flow)

In the region Д, where ~ ifi, x = 0(1), z = 0(1), and у = O(h0), we introduce stretching of the vertical coordinate

(2.7)

where h0 = const, is a characteristic magnitude of the ground clearance.[6] After substitution of x, z and у into the equations of the problem, we obtain the following formulation for the channel flow perturbation poten­tial <p:

, .2, d2m dy2 + rt0 V dx2 fo2 /

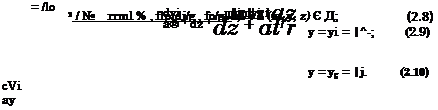In the channel flow region, both the condition at infinity (decay of pertur­bations in three-dimensional flow) and the Kutta-Zhukovsky condition at the trailing edge are lost. The influence of these conditions will be transmitted to the channel flow region by matching with the asymptotic solutions to be obtained in regions De and Du.

We seek <p in the form of the following asymptotic expansion:

<P і = Vi+f^Vi* = <Ph+<Pi2 К ln^- + <Ph h0 + h%<p**, {(fix, <p**) = 0(1),

° (2.П)

which can be shown to satisfy the requirement of matching of the asymptotic representations of the velocity potential in the regions Д, £)u, and De. Sub­stituting (2.11) in (2.8), yields the following equations for the functions <p* and <p**:

d2<p** d2ip* d2(p* dy2 = dx2 + dz2 ’

= 0, (x, y, z) Є A; (2.12)

Then, using the same asymptotic expansion (2.11) in the flow tangency con­ditions on the lower surface of the wing (2.9) and on the ground (2.10), we obtain the following set of equations:

• on the lower surface of the wing

Integrating (2.12) two times with respect to у and accounting for (2.14) and (2.16), we obtain an important conclusion: with an asymptotic error of the order of O(h0), the description of the channel flow is two­dimensional in the plane parallel to an unperturbed position of the ground surface, i. e., to the plane у = 0,

dtp* dy

<P* = ¥>*

dp* dy

Integrating (2.13) one time with respect to у, gives

, , t**t °Ч> тти\°Уі. , + э?>+/ <-*’^ = [-вї-Щк + – аГд; +

dip* j-r/.vi ayi a^j* ayi, <%

dyg | d(p*dyg

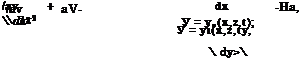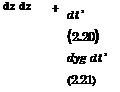where /**(x, z) is an unknown function. Taking into account equations (2.15) and (2.17), we obtain

(*, z) Є 5, (2.22)

Substracting (2.21) from (2.20), we obtain the following channel flow equa­tion:

where h* = h*(x, z,t)/h0 = y – yg, h*(x, z) = y(x, z) – yg{x, z) is the instantaneous distribution of the gap between the wing and the ground.

Thus, it has been shown that for very small clearances (an extreme ground effect), the flow field under the wing in the ground effect has a two-dimensional description and its perturbation velocity po­tential ~ (p* satisfies quasi-harmonic equation (2.22) in a two­dimensional domain S bounded by the wing planform contour.

The boundary conditions for (p* at the leading l and trailing edges I2 of the lifting surface will be obtained by matching.

From a physical viewpoint, equation (2.22) can be interpreted as the equa­tion of mass conservation in a highly constrained channel flow region with
known distributed mass addition due to tangency conditions on the lower surface of the wing and part of the ground situated under the wing.

For channel flow under the wake, the same procedures can be used to relate the induced downwash aw = O(h0) in the wake,

qw = = h0 + ^W2 In 7 + ^w3) (2.23)

to the wake channel flow potential <p[7] and the corresponding instantaneous gap distribution h^(x, z) = yw(x, z, t) – yg(x, z, t) by the following equation:

where = (yw – yg)/h0 = 2/w – 2/g.