Influence of the downwash on the tailplane

On most aircraft the tailplane is between the trailing vortices springing from the mainplanes ahead and the flow around it is considerably influenced by these trails. Forces on aerofoils are proportional to the square of the velocity and the angle of incidence. Small velocity changes, therefore, have negligible effect unless they alter the incidence of the aerofoil, when they then have a significant effect on the force on the aerofoil.

Tailplanes work at incidences that are altered appreciably by the tilting of the relative wind due to the large downward induced velocity components. Each particu­lar aircraft configuration will have its own geometry. The solution of a particular problem will be given here to show the method.

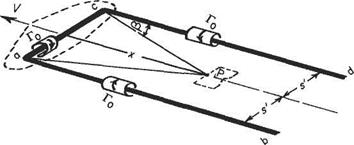
Example 5.1 Let the tailplane of an aeroplane be at distance x behind the wing centre of pressure and in the plane of the vortex trail (Fig. 5.16).

Assuming elliptic distribution, the semi-span of the bound vortex is given by Eqn (5.18) as

Fig. 5.16

The downwash at the mid-span point P of the tailplane caused by the wing is the sum of that caused by the bound vortex ac and that of each of the trailing vortices ab and cd. Using the special form of Biot-Savart equations (Section 5.2.2) the downwash at P:

wP J. = -^-2sin/3 ++cos/3)

4-їїх 4ns1

_ Гр (sin /3 1

27Г X

From the sketch x = s’ cot /3 and s’ = (n/4)s

Г0 ( sin /3 l+cos/3

2тг cot /З

= ^(1 +sec/3)

7TZS

Now by using the Kutta-Zhukovsky theorem, Eqn (4.10) and downwash angle

8 CL 7Г3(AR)

Wp

The derivative

дє _ де дСь _ дє да dCL да °l dCL

Thus

For cases when the distribution is non-elliptic or the tailplane is above or below the wing centre of pressure, the arithmetic of the problem is altered from that above, which applies only to this restricted problem. Again the mid-span point is taken as representative of the whole tailplane.

Ground

level

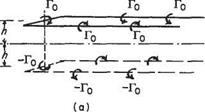
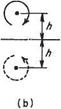
Fig. 5.17