Mach Number
The ratio of the speed of the flow to that of the speed of sound is called the Mach number and can be interpreted physically as a ratio of inertia forces in the fluid to forces resulting from compressibility. The speed of sound is the speed at which pressure disturbances are propagated through the air and is given by a = ffyRT where у — 1.4 is the ratio of specific heats for air, R is the gas constant, and T is absolute temperature. The speed of sound is approximately 1,117 ft s_1 (340 m s-1) at sea level on a standard day – see Section 5.2. When an airfoil travels at low speeds relative to the speed of sound, pressure disturbances travel at relatively high speeds in all directions. This causes the flow approaching the airfoil to change its velocity and pressure very gradually. The now, therefore, can be considered incompressible. Notice that for an truly incompressible flow a = oo, so that M = 0. When the airfoil travels at higher speeds relative to the speed of sound, disturbances cannot travel as far from the airfoil in a given time. This means that the flow approaching the airfoil undergoes more sudden changes. Under these conditions there are measurable changes to the characteristics of the airfoil, such as increased lift coefficient and a movement of the aerodynamic center. If the airfoil approaches and exceeds sonic speeds, then disturbances cannot be propagated upstream and discontinuous changes in the flow properties take place at the airfoil. Under these conditions there are large nonlinear changes in the airfoil characteristics.
|
(a) Moo reaches critical Mach number (b) M«, just greater than л/
|
|
|
|
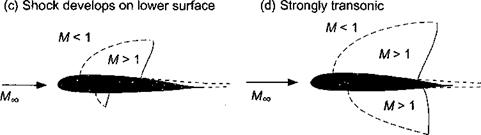
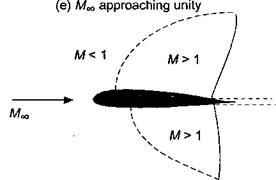
Figure 7.9 Development of supersonic flow pockets on an airfoil for increasing free-stream Mach number, (a) = critical Mach number, M*. (b) > M* with developing shock wave, (c) Shock wave develops on lower surface, (d) Lower surface shock wave moves quickly toward trailing edge, (e) MTO approaching unity. |
When the air flows past an airfoil, the local velocity at the surface outside the boundary layer may be greater or less than the free-stream velocity. The highest velocities occur near the leading edge and over the upper surface of the airfoil. If the free-stream velocity is low enough, the flow velocity remains subsonic everywhere. Such flows are relatively easy to analyze because the governing equations are linear. At higher free-stream velocities, however, the acceleration of the flow will eventually cause regions of supersonic flow. This is a mixed or transonic flow, which although predominantly subsonic, has an embedded supersonic pocket, as illustrated by Fig. 7.9. This problem is much more difficult to analyze because of the nonlinear nature of the equations governing the flow.
The value of the free-stream Mach number, Moo, where the flow first becomes locally sonic (M = 1) is called the critical Mach number, M*. The value of M* will also depend on the AoA of the airfoil. Further increases in Moo cause the extent of the supersonic region to grow, and the region becomes terminated by a shock wave that is initially almost perpendicular to the airfoil surface. Across the shock wave there is a rapid increase in pressure and also an entropy chalnge whereby energy is converted to heat resulting in
a form of profile drag known as wave drag. The interaction of the shock wave and the boundary layer results in an increase in skin friction drag. Moreover, the high adverse pressure gradients found in the vicinity of the shock wave make boundary layer thickening inevitable and this will be accompanied by an increase in profile drag.
With increasing Mach number (or AoA) the shock wave will strengthen, move aft, and become more oblique to the airfoil surface. At some point, depending on the AoA and airfoil shape, the flow on the lower surface also becomes supersonic, resulting in a second supersonic pocket and terminating shock wave. With further increases in M^, the lower surface shock wave moves quickly toward the trailing edge; this is followed by the rapid aft movement of the upper surface shock wave. If at any point during this process the shock wave becomes sufficiently strong, then the high adverse pressure gradients will cause the boundary layer to separate causing a loss of lift and an increase in drag known as shock induced stall. Liepman (1946) and Pearcy (1955) give good fundamental discussions on shock wave/boundary layer interactions.
In Fig. 7.1 it has already been shown that rotor airfoils operate in a relatively diverse aerodynamic regime during each revolution of the rotor, ranging from low subsonic speeds at the root of the blade to transonic flow conditions at the blade tips. Compressibility effects can manifest before sonic speed is reached locally on the airfoil. Even when the free-stream Mach number is quite low, say about 0.3 on the retreating blade, the high angles of attack found under dynamic (unsteady) conditions mean that a supercritical (locally supersonic) flow region can exist near the leading edge of the airfoil. Consequently, compressibility issues need tc be addressed very carefully to ensure that the selected airfoil sections will perform satisfactorily under the actual flight conditions found on a helicopter rotor.