Response of Luminescence to Time-Varying Excitation Light

6.1.1. First-Order Model

The lifetime method for PSP and TSP is based on the response of luminescence to a time-varying excitation light. The response of the luminescent emission I from a paint to an excitation light E(t) can be described as a first-order system

dl/dt = -1/t + E(t), (6.1)

where t is the luminescent lifetime. With the initial condition I(0) = 0, a solution to Eq. (6.1) is

I(t) = f exp[ -(t – u )/t ]E( u )du. (6.2)

Jo

For a pulse light E(t) = Am S(t), the luminescent response is simply an exponential decay

I(t) = Amexp( -1/t ). (6.3)

where m = 2kf is the circular frequency of the excitation light. Substitution of Eq. (6.4) into Eq. (6.2) yields the luminescent response after a short transient process

Here, the phase angles pn are related to the luminescent lifetime by

tan yn = nmx. (6.6)

In the simplest case where the sinusoidally modulated excitation light is E(t) = Am [1 + H sin( m t)] , the luminescent response Eq. (6.5) is reduced to

where Meff = (1 + x2 m2) 1/2 is the effective amplitude modulation index, Am is the amplitude, and H is the modulation depth. The phase angle ^ is related to the luminescent lifetime simply by

tan (p = rnx. (6.8)

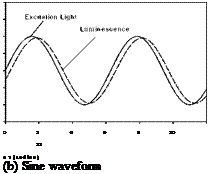
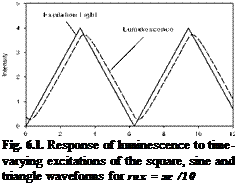
Other waveforms of the excitation light include square and triangle. Figure 6.1 shows the luminescent response to typical periodic excitations with the square, sine and triangle waveforms for the non-dimensional lifetime of юх = ж/10 .

2.5

2.0

>, 1.5

~ 1.0 0.5 0.0

4.0

3.5

3.0 .= 2.5 = 2.0

1.5

1.0

0.5

at (radian)

(c) Triangle waveform