ROBUST STABILITY (P1)

5 methods of chapter 5 are used, namely the mixed /і upper bound by Fan et al (subsection 2.3), the classical complex д upper bound (subsec­
tion 2.2), the real fj, upper bound by Zadeh and Desoer (subsection 1.1), the real Ц upper bound by Jones (subsection 1.3), and the real /л lower bound by Dailey (subsection 1.2). Note first that all these methods give nearly the same result (around 0.13) at u> = 0.

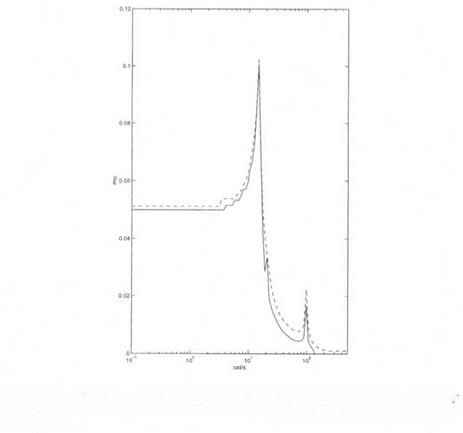Figure 6.1. Missile autopilot – robust stability (PI) – the real p upper bound b

Zadeh and Desoer is represented in dashed line and the real p lower bound by Dailey in solid line.

Figure 6.1 presents the real л upper bound by Zadeh and Desoer (dashed line) and the real p lower bound by Dailey (solid line). Note the good accuracy of the p interval at nearly all frequencies. The maximal value of the s. s.v. is obtained as 0.13 at ш = 0. The result is non conser­vative. The corresponding uncertainties in the stability derivatives are 5/0.13 « 40%. This means that the closed loop missile is stable despite simultaneous uncertainties of ± 40 % in the four stability derivatives. Note also the discontinuity of the p bounds by Zadeh and Desoer and by Dailey at u> = 0: д и 0.13 at w = 0, while p « 0.05 at very low
frequencies. This means that the exact value of the real s. s.v. is also discontinuous at the zero frequency, as already mentioned in (Ferreres et al., 1996a).

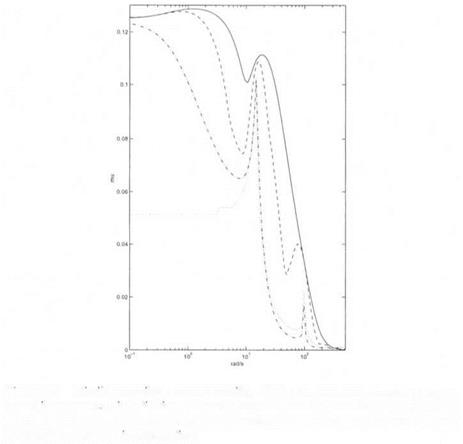Missile autopilot – robust stability (PI) – the classical complex /і upper

bound is represented m solid line, the real /і upper bound by Jones in dashed line, the mixed Ц upper bound by Fan et al in dasli-dotted line and the real ц upper bound by Zadeh and Desoer in dotted line.

Figure 6.2 presents the results obtained with the four p upper bounds (classical complex /x upper bound in solid line, real p upper bound by Jones in dashed line, mixed p upper bound by Fan et al in dash-dotted line, real p upper bound by Zadeh and Desoer in dotted line). This Figure illustrates the decreasing conservatism of these bounds. The best results are obtained with Zadeh and Desoer’s and Fan et al’s methods. More precisely, better results are obtained with Zadeh and Desoer’s method at low frequencies, equivalent results are obtained at medium frequencies, and better results are finally obtained with Fan et al’s method at high
frequencies. The classical complex // upper bound, the real // upper bound by Jones and the mixed //upper bound by Fan et al are continuous at = = 0 , unlike the real /і upper bound by Zadeh and Desoer.