The p Derivatives (Cyp, Clp, C„p)

When an airplane rolls with angular velocity p about its x axis (the flight direction), its motion is instantaneously like that of a screw. This motion affects the airflow (lo­cal angle of attack) at all stations of the wing and tail surfaces. This is illustrated in Fig. 5.12 for two points: a wing tip and the fin tip. It should be noted that the nondi­mensional rate of roll, p = pb/2u0 is, for small p, the angle (in radians) of the helix traced by the wing tip. These angle of attack changes bring about alterations in the aerodynamic load distribution over the surfaces, and thereby introduce perturbations in the forces and moments. The change in the wing load distribution also causes a modification to the trailing vortex sheet. The vorticity distribution in it is no longer symmetrical about the x axis, and a sidewash (positive, i. e., to the right) is induced at a vertical tail conventionally placed. This further modifies the angle-of-attack distri­bution on the vertical-tail surface. This sidewash due to rolling is characterized by the derivative da/dp. It has been studied theoretically and experimentally by Michael (1952), who has shown its importance in relation to correct estimation of the tail con­tributions to the rolling derivatives. Finally, the helical motion of the wing produces a trailing vortex sheet that is not flat, but helical. For the small rates of roll admissible in a linear theory, this effect may be neglected with respect to both wing and tail forces.

THE DERIVATIVE Cv

Ур

The side force due to rolling is often negligible. When it is not, the contributions that need to be considered are those from the wing[15] and from the vertical tail. The verti­cal-tail effect may be estimated in the light of its angle-of-attack change (see Fig. 5.12) as follows. Let the mean change in aF (see Fig. 3.12) due to the rolling velocity be

* Pzf, dcr

AaF =——– + p

u0 dp

where zF is an appropriate mean height of the fin. Introducing the nondimensional rate of roll, we may rewrite this as

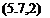/ zF da

д„,= -р(2–¥

The incremental side-force coefficient on the fin is obtained from Aah

Zf da

ДCVF = aF AaF = ~aFp ( 2 — —

where aF is the lift-curve slope of the vertical tail. The incremental side force on the airplane is then given by

thus

THE DERIVATIVE C,

lP

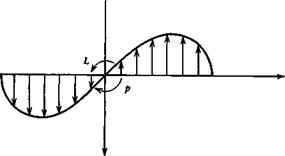
Clp is known as the damping-in-roll derivative. It expresses the resistance of the air­plane to rolling. Except in unusual circumstances, only the wing contributes signifi­cantly to this derivative. As can be seen from Fig. 5.12, the angle of attack due to p varies linearly across the span, from the value pb/2u0 at the right wing tip to —pb/2u0 at the left tip. This antisymmetric a distribution produces an anti-symmetric incre­ment in the lift distribution as shown in Fig. 5.13. In the linear range this is superim­posed on the symmetric lift distribution associated with the wing angle of attack in undisturbed flight. The large rolling moment L produced by this lift distribution is proportional to the tip angle of attack p (see Fig. 5.12), and Clp is a negative constant, so long as the local angle of attack remains below the local stalling angle.

If the wing angle of attack at the center line, aw(0), is large, then the incremental value due to p may take some sections of the wing beyond the stalling angle, as

Figure 5.13 Spanwise lift distribution due to rolling.

shown in Fig. 5.14. [Actually, for finite span wings, there is an additional induced an­gle of attack distribution a,(y) due to the vortex wake that modifies the net sectional value still further. We neglect this correction here in the interest of making the main point.] When this happens Clpp is reduced in magnitude from the linear value and if aw(0) is large enough, will even change sign. When this happens, the wing will au­torotate, the main characteristic of spinning flight.