The r Derivatives (Cyr, Clr, СПг)
 |
|
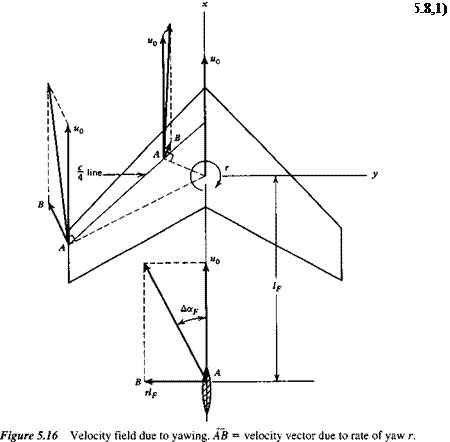
When an airplane has a rate of yaw r superimposed on the foward motion u0, its velocity field is altered significantly. This is illustrated for the wing and vertical tail in Fig. 5.16. The situation on the wing is clearly very complicated when it has much sweepback. The main feature however, is that the velocity of the chord line normal to itself is increased by the yawing on the left-hand side, and decreased on the right side. The aerodynamic forces at each section (lift, drag, moment) are therefore increased on the left-hand side, and decreased on the right-hand side. As in the case of the rolling wing, the unsymmetrical lift distribution leads to an unsymmetrical trailing vortex sheet, and hence a sidewash at the tail. The incremental tail angle of attack is then
THE DERIVATIVE Cyr
 |
|
The only contribution to СУг that is normally important is that of the tail. From the angle of attack change we find the incremental Cy to be
thus
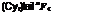
![]()
![]() (5.8,2)
(5.8,2)
THE DERIVATIVE Clr
This is another important cross derivative; the rolling moment due to yawing. The increase in lift on the left wing, and the decrease on the right wing combine to produce a positive rolling moment proportional to the original lift coefficient CL. Hence this derivative is largest at low speed. Aspect ratio, taper ratio, and sweepback are all important parameters.
When the vertical tail is large, its contribution may be significant. A formula for it can be derived in the same way as for the previous tail contributions, with the result
Sf? Zf I Ip da
«y.„ = «,T17(2T + 1f) <5ад
THE DERIVATIVE C„r
C„r is the damping-in-yaw derivative, and is always negative. The body adds a negligible amount to Cnr except when it is very large. The important contributions are those of the wing and tail. The increases in both the profile and induced drag on the left wing and the decreases on the right wing give a negative yawing moment and hence a resistance to the motion. The magnitude of the effect depends on the aspect ratio, taper ratio, and sweepback. For extremely large sweepback, of the order of 60°, the yawing moment associated with the induced drag may be positive; that is, produce a reduction in the damping.
The side force on the tail also provides a negative yawing moment. The calculation is similar to that for the preceding tail contributions, with the result
( If da
(CJtail = ~aFVv (2- + —) (5.8,4)












