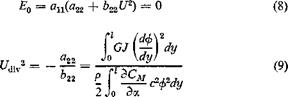THE STABILITY OF A DISTURBED MOTION

Let us now return to the general problem, and consider the stability of the motion of the cantilever wing of § 6.3 at any speed of flight U, following

an initial disturbance. The equation of motion is given by Eqs. 3 of § 6.3 and the boundary conditions by Eqs. 4 of that section. The solution can be expressed in the form

h = A f(y)eu, а. = Вф(у)еи (1)

where А, В, Я are constants; Z, f(y), ф(у) are to be determined by the differential system, and A, В by the initial conditions. To obtain an approximate solution, Galerkin’s method may be used. We shall assume approximate forms off(y), ф{у) to be known (as discussed in § 6.4). Let us substitute Eqs. 1 into Eqs. 3 of § 6.3, multiply the first equation by f(y) and the second by ф(у), integrate both with respect to у from 0 to /, to obtain two linear homogeneous equations for A and B, which are exactly the same as Eqs. 3 of § 6.4, except that the factor /со in those equations must be replaced by Z. For a nontrivial solution corresponding to a disturbed motion, the determinant of the coefficients of A and В must vanish. This determinantal equation, known as the characteristic equation, may be written as

A0№ + B0P + QA* + D0Z + E0 = 0 (2)

where

A о = A j, B0 = BjU

C0 = C, + C2U2, D0 = D, U + D2U* (3)

E0 = Щ. -!- E2U2,

and Ab Blt etc., are given by Eqs. 6 of § 6.4.

From the discussion in § 6.3, it is seen that the condition for stability of the disturbed motion is that the real parts of all the roots of the characteristic equation be negative. The necessary and sufficient con­dition for this is that the coefficients A0, B0, C0, D0, E0 and the Routh discriminant

R = B0C0D0 – B02E0 – D2A0 (4)

have the same sign.* It can be shown on the basis of Schwarz inequalityf

* See Appendix 2.

t For arbitrary functions f^x) and/2(ж), we have

J[a /)(*) 4- Д/2(ж)]г dx > 0 i. e.

“2l/i2(®) dx + /і(ж) /2(ж) dx + dx^O

Since this is a positive definite function of a,(3, the discriminant must be negative, which leads to Schwarz inequality

lifX*) dx][$ff(x) dx] > Шх)/2(х) dx?

that the coefficient A0 is always positive. Hence the conditions of stability are

B0 > 0, C0 > 0, D0 > 0, E0 > 0, R > 0 (5)

These inequalities are satisfied when U is very small, because it is shown in § 6.3 that the disturbed motion is stable. As V increases, the coeffi­cients B0, C0, • ■ R vary. Since B0 = BflJ and B1 does not depend on U, B0 is positive at all values of V > 0. As for C0 and D0, we shall show that E0 and R become zero before C0 and D0. For, if D0 = 0, then

R = – W (6)

which shows that either E0 or R must be negative. Similarly, if C0 = 0, then

r = — ад – ад (7)

which again shows that either E0 or R must be negative. Hence, as long as Eq and R remain positive, C0 and D0 must be positive.

The stability is then determined by the signs of E0 and R. If E0 and R0 remain positive, the motion is stable. If either one becomes negative, the motion is unstable.

The physical meaning of the critical condition E0 = 0 or R = 0 can be clarified as follows. When Eq = 0, Eq. 2 has a root Я = 0. Hence, according to Eqs. 12 of § 6.3, a condition of wing divergence is reached. The divergence speed is given by

which agrees with the result of § 3.4, CM being the coefficient of aero­dynamic moment about the elastic axis.

The condition R = 0, on the other hand, corresponds to the critical flutter condition. For, a substitution of A0, B0, etc., from Eqs. 3 leads to

R = иьт – г МІР + N) = 0 (10)

which is exactly the critical flutter equation 8 of § 6.4, except for the factor Vz. That Eq. 10 has a root U — 0 simply reflects the fact that the structure may oscillate in still air, which is a natural consequence of our assumption that the viscosity of the air and the internal damping of the structure are negligible.

Combining the above results with the discussion at the end of § 6.3, we see that, at U slightly larger than the smallest critical flutter speed, the motion will be unstable if R < 0. The very special case that R becomes zero at Ua but becomes positive again at supercritical speeds occurs only when R reaches a relative minimum at Ua. This is possible if and only if[18]

(11)

Using Eq. 10, we see that the dimensions and the aerodynamic character­istics of the wing must be such as to satisfy the conditions

M2 = 4LN and M < 0 (12)

If Eq. 12 is satisfied, then the critical nature of the motion at the speed Uct is only superficial. For, at speeds differing slightly from UCI (either larger or smaller), the disturbed motion is stable. If Eq. 12 is not satisfied, then the speed Uct is truly critical; for supercritical speeds the motion diverges. The exacting condition 12 has little chance of being satisfied in practice.

This method of stability investigation can be applied to other aero – elastic systems whenever the time variable appears in the governing equation as derivatives of finite order (see footnote, p. 228). The general method consists of deriving a characteristic equation by a substitution such as Eq. 1, and then check the signs of Routh or Hurwitz discriminants (Appendix 2).