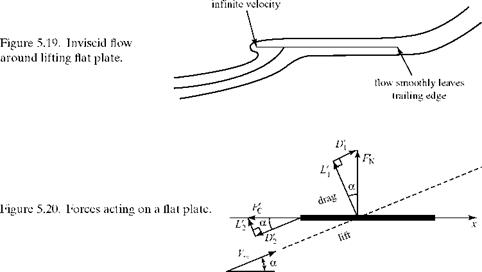
The Symmetrical Thin Airfoil

_L Г Y 2 n0(*- ^

In this case, the mean camber line and the chord line coincide. Thus, when the thick­ness is stripped away, the airfoil is a flat plate and the vortex-sheet representation is along the chord so that the planar-boundary-condition approximation becomes exact. Furthermore, for the symmetric airfoil, dz / dx = 0, and Eq. (5.6) becomes:

It is convenient to make a change of variable to perform the integration. Let:

c

= 2(1 – cos0),

where 0 is the new running variable. The fixed point in question, x, is denoted by:

x = 2(1 – cosФ).

This change of variable is equivalent to specifying chordwise location by angular rather than linear measure. Imagine a circle of radius c/2 centered at mid-chord (Fig. 5.16).

c

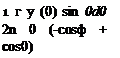At the limits of integration, x = 0 ^ 0 = 0 and x = c ^ 0 = n. Finally, d^ = — sin0d0 . Then, the defining equation for a symmetric airfoil, Eq. 5.7, may be written as follows:

This equation may be solved by integral-equation techniques that are beyond the scope of this text. The result is:

The claim that this is the solution may be verified by substituting Eq. 5.11 into the integrand of Eq. 5.10); namely: Evaluating the integral in Eq. 5.12b requires that we address the singular behavior of the integrand at 0 = ф (i. e., when the running variable is at the point in question, £ = x). This is done by using the “principal value” of the integral (see Appendix E in Abbott and Van Doenhoff (1959)):

where n may be 0, 1, 2, . . . depending on the form of the integrand. In the case of interest here, n = 0 and n = 1 in Eq. 5.12b. Thus, Eq. 5.12b becomes:

aV

—- [0 + n] = Va n –

and the solution, Eq. 5.11, was verified.

Notice also that if Eq. 5.11 is the solution, then it must exhibit the proper behavior at the trailing edge, 0 = n. At the trailing edge:

which is indeterminate. However, using L’ Hopital’s Rule (recall that the numerator and denominator are differentiated within the limit):

Thus, Y(n) = 0 and the Kutta condition is satisfied.

At the leading edge, 0 ^ 0 and Eq. 5.11 indicates that the vortex-sheet strength becomes infinite. This is allowable because the Kutta condition makes no demands on leading-edge behavior. The leading edge of even a thin airfoil is rounded, and the flat or curved plate representation of the airfoil simply breaks down at this single point. This is interpreted here as a limiting representation of what is called leading – edge suction, the low pressure (i. e., high velocity) caused by the flow rapidly accel­erating around the leading edge of an airfoil from the bottom to the top surface. The vortex-sheet strength then has the general characteristics depicted in Fig. 5.17. Having verified the solution, Eq. 5.11, we now can determine the expressions for the lift and moment coefficients for the symmetrical airfoil.

Figure 5.17. Vortex-sheet-strength distribution.

The lift coefficient is found by (1) appealing to the Kutta-Joukowski Theorem, and (2) finding the pressure distribution over the plate and then integrating. The fact that the two results are identical serves as further verification of the vortex theory of lift.

1. The total circulation around the airfoil is found by summing all of the contribu­tions due to the vortex elements—namely:

c П

r = J Y(£)d£ = C j у (0) sin Ш

0 2 0

after the change of variable. Substituting the solution, Eq. 5.11, into this inte­grand yields:

Г = caVrj (1 + cos0)d0 = canVr.

0

The Kutta-Joukowski Theorem then states that the lift per unit span is:

L’ = pVT = pVfcna

and the two-dimensional lift coefficient is:

The quantity unity in the denominator is a reminder that L’ is the lift per unit span.

2. The lift coefficient now is found by integrating the pressures acting on the sym­metrical thin airfoil (i. e., flat plate). These pressures always act perpendicular to the surface (Fig. 5.18).

At first glance, Fig. 5.18 is puzzling. It indicates that the net pressure force on the plate acts in the z-direction; that is, it acts as a force normal to the chord. Then, this normal force apparently can be decomposed into two forces: one perpendicular to the freestream direction and the other parallel to the freestream direction. By defi­nition, the force perpendicular to the freestream direction is the lift force. Also by definition, the force component parallel to the freestream direction is the drag force. However, there can be no drag force in a two-dimensional, inviscid flow, as indicated in D’Alembert’s Paradox. There can be neither frictional nor pressure drag because no boundary layer is represented in the inviscid model.

The answer to this apparent contradiction is that there is another force acting on the plate—namely, a suction force at the leading edge acting in the chordwise (i. e., x-axis) direction. Recall that there is no boundary condition imposed at the leading edge, such as the Kutta condition at the trailing edge, and that this presents no practical problem because even thin airfoils have rounded leading edges with no anomalous velocity behavior. However, in the analytical model, in the limit of zero thickness, the inviscid flow has an infinite velocity as it accelerates around the sharp leading edge of the flat plate (Fig. 5.19). This infinite velocity produces an infinite negative pressure (i. e., suction) at the leading edge (according to the Ber­noulli Equation), and this infinite suction acts on a zero-thickness plate. In the limit, the product of the infinite suction per unit area acting on an infinitesimal plate area is a finite force in the chordwise upstream (i. e., thrust) direction. The forces acting on the flat plate then are as shown in Fig. 5.20, where F ‘N is the normal force per unit span and F’ C is the chordwise force per unit span. In the figure, each of these two forces is decomposed into lift and drag components.

From Figs. 5.18 and 5.20, it follows that:

c 1 T/2 1 T/2

FN = J(pL – Pu)dx and Pl~ po – 2pVL ; pu _ Po – 2pVu,

0

where Bernoulli’s Equation was used. Because the stagnation pressure, p0, is con­stant throughout the flow, we find that:

As previously noted, (Vu – VL) = y, so the first term in the integrand is the local vortex-sheet strength. Also, by applying the exact Joukowski-transformation method discussed in the last section to the special case of flow around a flat-plate airfoil, it may be shown that:

Thus,

c

FN= pV^cosa J jdx =pV^r cos a. (5.16a)

0

Notice that Eq. 5.16 does not state that exactly F’N = рУ^Г, nor should it because it is an expression for the normal force, not the lift force, per unit span.

Rather than pondering how to evaluate the product of an infinite pressure and an infinitesimal area, a simpler approach is to argue that in this two-dimensional, inviscid flow, the drag force on the plate must be zero. That is, D – D’2 = 0, where a positive drag force is in the streamwise direction, so that D’ 2 = DFrom Eq. 5.16a and Fig. 5.20:

D[ = FN sin a = (рУмГ cos a) sin a.

D’

Furthermore, from geometry, —L = cos a. Solving for F’ C and substituting for D 2 = D’ 1

, Г cos a)sin a,

FC =^-^—————- = (pV Г)sin a.

C cos a ”

Finally, we recognize that the total lift on the plate is given by L’ = L’ 1 + L’2, so that:

L’ = FN cos a + FC sin a.

Substituting from Eq. 5.16:

L’ = pVM(cos2 a + sin2 a) = pV^r,

which agrees with the Kutta-Joukowski Theorem result, and the vortex theory of lift is verified. Finally, using Eq. 5.15, Q = 2na.

Thus, according to thin-airfoil theory, for a symmetrical airfoil, the airfoil lift coefficient is given by:

and the corresponding lift-curve slope is:

These equations state that the lift coefficient varies linearly with the angle of attack. It is shown later that this prediction is in excellent agreement with experimental data at moderate angles of attack before flow-separation effects begin to dominate and stall is approached. This can be seen for the special case illustrated in Fig. 5.3: The linear behavior applies to the unflapped NACA 4415 airfoil in the angle-of-attack range -10 ° < a < 10 °.

Notice in Eq. 5.17 that because the lift coefficient is dimensionless, the angle of attack must be in radians, which also is a dimensionless quantity. Eq. 5.17a is some­times written as Cg = m0a, where m0 is the lift-curve slope in radians. The coefficient, m0, may be assigned its theoretical value, m0 = 2n, or it may be determined from experimental, two-dimensional test results. Alternately, Eq. 5.17a may be written as Q = a0a, where a0 is the lift-curve slope per degree (i. e., thin-airfoil-theory result:

0. 11 per degree) and the angle of attack then is written in degrees.

The airfoil pitching moment may be found about any point on the chord line and then transferred to any other point. For convenience, the pitching moment per unit, span, M’, is taken about the airfoil leading edge as shown is Fig. 5.21. The moment may be evaluated either by summing up the contribution due to each element of the vortex sheet or by evaluating the moment due to the pressure distribution on the airfoil (i. e., plate). The latter approach is more physical and is used here.

Let a clockwise moment about the leading edge be positive. Then, the moment about the leading edge due to a pressure difference over an interval dx, at any dis­tance x from the leading edge is obtained by integration—namely:

c

MLE = – J (PL – Pu)xdx.

0

The minus sign is introduced because if PL > PU, the moment contribution is coun­terclockwise and therefore must be negative.

In the development of Eq. 5.16a, it is shown that (PL – PU = pyE^ cos a. Because the angle of attack is small, this can be approximated by:

(Pl – Pu) = PY

and the small angle approximation is used wherever needed. Then, we use Eq. 5.11 for the vortex-sheet strength, y, and the transformation to angular measure from

z
Figure 5.21. Pitching moment about		Pu
the leading edge.	+
	У ,	dx ‘
	x	Pl

Eq. 5.8. Writing the variable of integration in the moment definition as E rather than x to emphasize that it is a dummy integration variable:

Notice that for the moment coefficient to be dimensionless, the definition must con­tain a length squared in the denominator because the numerator now contains a lever-arm length. Also, notice that at positive angles of attack, the airfoil pitching moment is negative or clockwise; hence, it is a nose-down pitching moment, or a so – called restoring moment.

Two other properties of the symmetrical airfoil can be deduced from Eq. 5.18. Recall from Section 5.1 that the center of pressure is the point on the airfoil about which the moment is zero. We multiply both sides of Eq. 5.18 by (q^c2), which gives:

ML e = – 4 L’.

This result states that lift is the only contributor to moment and that the integrated lift force can be interpreted as a point force with its line of action at the quarter – chord point, as shown in Fig. 5.22. Thus, at the point c/4, the lever arm of the lift force is zero and the moment about that point is zero. It follows that the quarter-chord point of the symmetrical airfoil is the center of pressure.

Also recall from Section 5.1 that the aerodynamic center is the point on the airfoil where the moment is independent of the angle of attack. From Eq. 5.17a, the lift varies with the angle of attack. Because lift is the only contributor to moment, then the only point on the airfoil where the moment is independent of the angle of attack is the point where the lift-force lever arm is of zero length. Again, this is the

quarter-chord point. At this point, the pitching moment is not only independent of the angle of attack, it also is zero. Thus, for a symmetrical thin airfoil, both the center of pressure and the aerodynamic center are located at the quarter-chord point.

The Cambered Thin Airfoil

± r y(S№ V 2(*- k) “

The cambered-thin-airfoil problem requires that the vortex-sheet strength be found from Eq. 5.6, given the angle of attack and the equation of the mean camber line. Thus, the following integral equation must be solved for y(x):

As in the symmetrical-airfoil case, it is more convenient to cast this equation in angular measure, as in deriving Eq. 5.10. Thus, Eq. 5.6 becomes:

_L Г Y(в)sin0d0 = V L Jdz

2^0 (-cos ф + cos 0) v dx,

where 0 is an integration variable, ф designates the fixed point in question, and dz / dx is the slope of the mean camber line evaluated at the point in question. The solution for the vortex-sheet strength, y (0), in Eq. 5.19 is subject to the Kutta con­dition, y (n) = 0.

A solution to Eq. 5.19 is sought by applying a Fourier-series approach. We realize that because the cambered airfoil is represented as an airfoil of zero thickness (i. e., a curved flat plate), the vortex-sheet strength for the cambered airfoil must have the same general character as the distribution shown in Fig. 5.17 for a symmetrical airfoil; namely: Y (x) must be zero at the trailing edge and infinite at the leading edge. Now, recall from engineering mathematics that any curve or function may be represented over an interval by an infinite series comprising both sine and cosine terms—that is, a Fourier series.

For the current problem, the interval is from the leading edge (0 = 0) to the trailing edge (0 = n). In this problem, the cosine terms in the Fourier series are omitted because they would violate the Kutta condition—that is, the cosine terms would make a nonzero contribution to the source strength at the trailing edge, 0 = n. Thus, we represent the vortex-sheet distribution by the Fourier sine series as follows:

Y(0) =X Aisin n0. (5.20)

n=0

Now, the flow velocity and the vortex-sheet strength must be infinite at the leading edge of the cambered airfoil as in the symmetrical airfoil. To ensure the proper behavior at the leading edge, the first term of the series in Eq. 5.20, (n = 0), is written as a “flat-plate” term given by the symmetrical airfoil solution in Eq. 5.11. Some
generality is retained by writing the coefficient A0 in place of a. Then, the solution to Eq. 5.19 is represented by the Fourier series as follows:

Y(9) = 2 V a/1 + c°s 9) + 2 V У An sin и0. J sin9 “ПГі "

The coefficients An in the terms of the series n > 1 appearing in Eq. 5.20 were replaced by 2V“An in Eq. 5.21 to make a common multiplier (2V“ appear in all of the terms in Eq. 5.21. The constant value (2V“ simply is absorbed in the definition of An in the summation part of Eq. 5.21.

Of course, Eq. 5.21 is a solution only if there is a mechanism by which to solve for the coefficients of the series. This mechanism is supplied by imposing the boundary condition that the mean camber line must be a streamline. When the solution is completed, it should contain the symmetrical airfoil as a special case—namely, that A0 must equal a and all of the other An’s must be zero.

Substituting Eq. 5.21 into Eq. 5.19 yields:

1 П ATl + cos9)d9 1 A, sinn9sm9d9 (dz]

— I—————- + — І У —————– = a- —

п0 cos9-созф п0n=1 cos9-cosф ^dx,

The first term can be integrated directly by using the “principal value” as given by Eq. 5.13. The second term can be written in a form suitable for integration by appli­cation of the principal value in Eq. 5.13 if the numerator is written in terms of cosines by using the trigonometric identity:

sin n9sin 9 = 1 / 2[cos(n -1)0 – cos(n+1)9].

Substituting and integrating Eq. 5.22 leads to:

1

A0 + —{ A1(0) + A(n) +

The student should verify this result. Thus, on integrating, Eq. 5.22 can be written as:

= a – A0 + У An тоs пф. (5.23)

n=1

Eq. 5.23 provides the mechanism for evaluating the An’s. The equation must hold at any chordwise station, x, at which station the left side is known and the angle ф is determined by the transformation x = (c/2)(1-cos ф). Notice that Eq. 5.23 also could be written in terms of 9 as ф because both angles correspond to “a chordwise station.” The two angles must be distinguished carefully only when they both appear together in an integrand.

The An’s in Eq. 5.23 are solved in two steps, using standard Fourier-series tech­niques, as follows:

1.

Solve for A0: Integrate Eq. 5.23 over the interval (0 – n); namely:

because over this interval:

П

J (A cos яф^ф = 0

0

for all n. Rearranging:

A =a– Jdzdф. (5.24)

0 n 0 dx

In this equation, the camber-line slope can be expressed as a function of the angle ф through the change of variable expression (see Example 5.1).

2. Solve for the remaining An’s. Multiply both sides of Eq. 5.23 by cos тф, where m is a dummy counter, and again integrate over the interval:

J —z cos mdФ = J (a – A)) ros mфdф + J ^ (An cos пф) cos mфdф = L^ +12.

0 dx 0 0n=1

П

From calculus, I1 = 0 for all values of m, whereas I2=0 when n Ф m and I2= —An

when n = m. 2

Using these facts and rearranging:

An = — f —z (cos пф^ф (n > 1). (5.25)

n п 0 dx

The vortex-sheet-strength distribution for the cambered thin airfoil now is known because Eqs. 5.24 and Eq. 5.25 provide the mechanism for evaluating the coefficients in the Fourier-series expression for у(0) = у(ф) in Eq. 5.21. Notice that the vortex – sheet strength depends on the local slope of the mean camber line because the slope appears in both coefficient equations. Also, note that for a symmetrical airfoil, A0 = a, and all of the other An’s are zero so that Eq. 5.21 reduces to the prior result for the symmetrical airfoil in this special case, as expected.

If the chordwise pressure distribution on the airfoil is required, all of the An’s must be found. Evaluating the aerodynamic coefficients is less demanding and the expressions for these coefficients are now determined.

Lift Coefficient

We recall that:

c П

Then, we substitute for у (9) the Fourier-series expression, Eq. 5.21, so that:

П П m

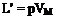і A. a + cos 9)d9 + IX An sm n9 sin 9d9 I.

0 0 n=1 _

These two integrals may be evaluated using basic trigonometric identities and inte­gral tables. The result is as follows:

Q = 1Тс = П(1 A^ + A1)- (5-26)

Notice that the value of the lift coefficient depends on both the angle of attack and the camber of the airfoil and that only two Fourier coefficients need to be evaluated. Substituting for A0 and A1, Eq. 5.26 may be written as:

where в is an angle (in radians) whose magnitude (a constant for a given problem) only depends on the camber of the airfoil, a geometric property of the airfoil shape. From Eq. 5.27, the following facts emerge:

1. The lift-curve slope for an arbitrary thin airfoil is:

dC„

—1 = 2 n, (5.28)

da

which is the same expression as for a symmetrical airfoil.

2.

When the geometric angle of attack has the value a = – p, the lift coefficient (and the lift) is zero. This special angle of attack only depends on the character of the airfoil camber and is called the angle of zero lift, aLo. Setting Q = 0 in Eq. 5.27, the magnitude of this angle (in radians) is given by:

The angle of zero lift is always negative for a positive-camber airfoil.

3.

A new angle of attack, the absolute angle of attack aa, now may be defined from Eq. 5.27 with p set equal to – aL0. Thus,

Examine Fig. 5.23. If an airfoil has positive camber, then when the geometric angle of attack, a, is zero and the chord line is coincident with the flow direction, the lift coefficient is greater than zero. It is necessary to use a negative geometric angle of attack when the zero lift line (ZLL) is aligned with the flow to make the lift coefficient zero. The angle between the chord line and the ZLL is the angle of zero lift, a quantity that usually carries a negative sign. The absolute angle of attack is the angle between the oncoming flow and the ZLL. Notice also that the angle of zero lift is zero for a symmetrical airfoil.

Figure 5.23. Absolute angle of attack.