Vortex-Sheet Representation of a Thin Airfoil

An analytical solution for the vortex-sheet strength is not possible for an airfoil of arbitrary thickness ratio. Full numerical solutions were developed, as discussed in Section 5.7. However, an analytical solution can be constructed if the vortex-sheet model is applied to thin airfoils. If an airfoil is thin (i. e., 10 to 12 percent thickness ratio or less), then the vortex sheets on the airfoil upper and lower surfaces are close to the mean camber line. This fact can be approximated by distributing the vortex sheet along the airfoil mean camber line. This entails stripping off and discarding the symmetrical thickness distribution above and below the mean camber line, leaving only the mean camber line to represent the airfoil as shown in Fig. 5.12.

This approach provides results that are in good agreement with experiments for thin airfoils. The exact solution for a Joukowski airfoil discussed previously showed that the influence of thickness on lift and moment coefficient is minor if the thick­ness ratio is small. It is appealing to replace the mean camber line with a vortex sheet, because there is a jump in velocity across the vortex sheet as there would be across a mean camber line representing the airfoil because the mean camber line then is a streamline. Thin-airfoil theory represents a symmetrical airfoil as a flat plate and a cambered airfoil as a curved plate.

Again, the vortex-sheet strength as a function of chordwise distance is found by imposing the Kutta condition as well as the condition that the mean camber line must be a streamline (i. e., no flow component normal to the camber line). The circu­lation and the lift per unit span follow.

The uniqueness of the circulation about the airfoil as a function of angle of attack is a result of the Kutta condition. Recall from Section 4.9 that for a finite trailing-edge angle, the Kutta condition demands that the trailing edge be a stagna­tion point; whereas for a cusped trailing edge, the condition demands that the flow exiting the trailing edge at the upper and lower surfaces has the same velocity. At the trailing edge of the camber line, let the velocity be V. Thus, at the trailing edge (i. e., finite angle), Vy = VL = 0 or (cusp) Vy = VL. Recalling that the local sheet strength was shown to be equal to the local jump in velocity across the sheet, у = (Vy – VL), it follows that in either case, y(TE) = 0. The other condition on у(s) is that the mean camber line must be a streamline.

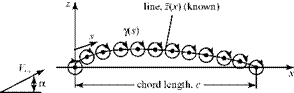
Consider a thin airfoil at angle of attack and represented by a vortex sheet dis­tributed along the mean camber line. Place the airfoil in a body-axis coordinate

system (Fig. 5.12) with the x-axis aligned with the chord line. The equation of the mean camber line, z(x), is known. The vortex-sheet strength, у (s), is determined and then used to find the pressure distribution, Cp(x); the lift coefficient, Q ; and the pitching moment coefficient, Cm.

If the mean camber line is to be a streamline, there can be no flow through the vortex sheet. This means that at every point along the vortex sheet, the velocity component, V(s), is perpendicular to the mean camber line (see Fig. 5.13). V(s) is induced by all other elements of the vortex sheet. It must be equal and opposite to the normal component of the freestream velocity, V*n, which is normal to the mean camber line at that point. Thus, V(s) + V*n = 0 at every point along the mean camber line, as shown in Fig. 5.13.

Formulate V*n by expressing V*n in terms of the slope of the mean camber line at any point. The slope of the mean camber line is given by dz/ dx, which is a known. Then, the angle 5 = tan-1(-dz / dx), where the minus sign is added to keep the sense of the angle correct. That is, when the camber-line slope, dz/dx, is negative, then (a + 5) should be additive, as shown in Fig. 5.14. Near the front of the airfoil, when the mean camber-line slope is positive, the opposite is true.

V* n= V* sin(a + 5) = V^sin

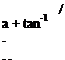From Fig. 5.14:

V = V * n *

For a thin airfoil at a moderate angle of attack, this may be approximated as:

It remains to derive an expression for V(s) to complete the boundary-condition statement.

Finding the expression for V(s) is not particularly straightforward because V(s) is the resultant velocity induced at a point on the curved sheet by all of the other elements of the sheet. Thus, referring to Fig. 5.9(b), the Point P now is on the sheet

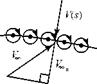
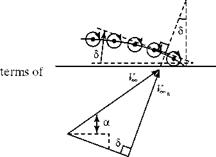Figure 5.13. The camber-line boundary condition.

Figure 5.14. The streamline boundary condition in camber-line slope
but the line r from each element of sheet ds to the Point P has a different orientation in the general case of a curved sheet. In addition to determining each slant distance, r, this means that each dV induced by y ds at Point P is at a different angle. The complexity is overcome again by taking advantage of the thin-airfoil geometry. We realize that if the thickness ratio is small, then the maximum camber ratio must be even smaller (i. e., a few percentage points), and the mean camber line is not far from the chord line—that is, the x-axis. Thus, only a small error results if the vortex sheet is placed along the chord line and the induced velocity is evaluated there. We assume in effect, that s ~ x and V(s) ~ V(x). This approximation is termed satisfying the boundary condition in the plane, a method that is often used in similar geometrical situations. Remember that even though the induced velocity is evaluated along the x-axis, the theory still insists that the mean camber line be a streamline. That is, the sheet strength is evaluated by demanding that the mean camber line be a streamline, not that the chord line be a streamline. This approximation greatly simplifies the geometry that enters the induced velocity calculation, as indicated in Fig. 5.15.

Recalling from the previous discussion of the vortex sheet that the induced velocity dV = – y ds/2nr, it follows from Fig. 5.15 that:

here the integration sums all of the dV at an arbitrary (but fixed) point, x, induced at that point by the element of the vortex sheet at the location S. Here, S is a running variable that disappears on integration. Notice that the integrand is singular (i. e., blows up) at x = S. (This is addressed later.) Remember that even though this V(x) is perpendicular to the chord line, it is treated as if it were perpendicular to the mean camber line. Thus, in the boundary-condition expression, V(x) is set equal and oppo­site to Vron at the mean camber line—namely, V^n + V(x) = 0.

_L Г Ж№ = V 2n0(*“S) “

Assembling Eqs. 5.4 and 5.5, the boundary condition requires that at any arbi­trary (but fixed) chordwise station:

Eq. 5.6 is the basic equation of thin-airfoil theory. The right side is known because the angle of attack must be given and the mean camber line is specified for a given airfoil so that dz/ dx can be found. Eq. 5.6 represents an integral equation for the unknown y (x) and must be solved subject to the Kutta condition that y(c) = 0, as described in Chapter 4.

The symmetric thin airfoil and the airfoil with arbitrary camber are examined in the next two sections. The appeal of thin-airfoil theory is that it provides a com­pletely analytical solution; the disadvantage is that it applies only to thin airfoils. Applying the results to airfoils thicker than about 12 percent thickness ratio leads to increasingly larger errors when compared to experimental data.