Wave drag of arbitrary slender bodies of revolution

The control-volume wave drag analysis of a 2D airfoil, which gave result (8.138), extends readily to the axisymmetric body of revolution. The result is

Dw = – pxVi//фг фх dS (8.152)

where the integral area element dS is on a cylindrical “pipe” surface surrounding the body and aligned with the freestream. The potential p can be obtained by the line-source superposition integral (8.145). Ashley and Landahl [50] combine these two expressions and give after some manipulation

where body extends over x = 0… l. Note that the drag depends on the square of dA/dx = d2A/dx2, so that low wave drag dictates bodies which have smooth cross-sectional area distributions. This is one example of Whitcomb’s supersonic area rule, discussed in detail by R. T. Jones [61].

Bodies with minimum wave drag

Following Sears [62] and Haack [63], the line source model developed above will now be applied to a body of length l, with some arbitrary area distribution A(x). Using the trigonometric coordinate d(x)

l l

x = – (1 — cost?) , dx = – sind dd (8.154)

the line source strength or equivalently dA/dx is expanded in a Fourier sine series.

о 2 о 16 The n = 1 series term has been excluded because it gives a finite base area at x = l. In reality the large separated wake generated by the base area would make the present potential-flow model results not very realistic for that case.

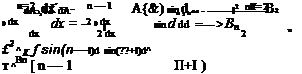The area distribution A(x) and the total body volume V can then also be given in terms of the same series coefficients.

Substitution of the source strength expansion (8.155) into the wave drag expression (8.153) gives the fol­lowing result, obtained by Sears.

nBn

8 n=2

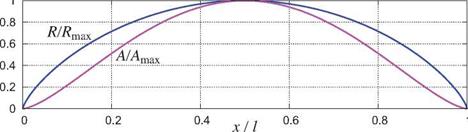
Comparing the volume expression (8.157) with the wave drag expression (8.158) we see that the lowest wave drag for a given body volume V and length l is obtained by setting B3 = B4 … = 0 and leaving only B2 nonzero. The resulting shape is the Sears-Haack body, shown in Figure 8.25. Note that its wave drag is independent of the freestream Mach number, provided of course that is sufficiently far into the supersonic range as required by the assumed supersonic PG flow model.

The very strong dependence of wave drag on the volume and the inverse length is the primary reason why the design of supersonic aircraft naturally favors a long and slender layout with minimal volume. These design drivers are not present in subsonic aerodynamics.

Figure 8.25: Sears-Haack body shape R(x) which gives minimum supersonic wave drag for given length and volume. Corresponding body cross-sectional area A = nR2 is also shown.