Algorithm for High Incidences—Regularization of the Solution

In relation to Fig. 10.11, with decrease in TSR or equivalently with increase in adv, the incidence of the blade element increases. When a j > (a)Clmax, the sign of the lift slope changes to ‘a < 0, which destabilizes the algorithm. This simply reflects that multiple values of a exist for a given Cl, therefore it is necessary to regularize the solution to make it unique. This can be done by adding an artificial viscosity term to the right-hand-side:

1

Гj — —2qjcjCi(aj) + Mj(Гj+1 — 2rj + Гj-1); j — 2,…, jx — 1 (10.93)

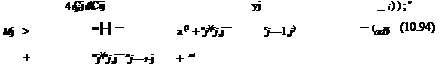where mj > 0 is the artificial viscosity coefficient. A test case with exact solution, based on the lifting line theory of Prandtl and a 2-D lift coefficient given analytically by Cl (a) — n sin 2a, for a wing with elliptic planform and equipped with a sym­metric profile, has shown that this approach gives excellent results for the complete range of a’s, from zero to § [12]. The artificial viscosity coefficient is given by

and the equation now reads

cj dCij / yj _

1 + 2d~a l(1+uj)(Cj,] — Cj—1,]) — (adv+wj)(a;] — aj—1’] + aj,]7 + 2m

— —2 qjCjCi (aj) — rj + Mj (Г+ — 2Гп + Г”—1) (10.95)

Now, the relaxation factor needs to be reduced to a value less than one, say ш — 0.3, depending on the polar smoothness. The need for the smoothing term is highlighted with a calculation of the two-bladed NREL rotor [1] at TSR — 3.8. The S809 profile that equips the blade is represented by the viscous polar calculated with XFOIL [13], for which one finds (a)Clmax — 17.5°. At this low TSR the blade is stalled from y — 0.35 to almost y — 0.6. The blade elements working conditions for the converged solution obtained with the artificial viscosity term are shown in Fig. 10.15 with the profile polar.

The circulation and incidence distributions, although converged for m — 0, show large oscillations which are unphysical, Fig. 10.16.