Boundary Conditions

For the beam-bending problem, it is necessary to impose two boundary conditions at each end of the beam. Mathematically, boundary conditions may affect v and its partial derivatives, such as dv/dx, d2v/3×2, d3v/3×3, d2v/3t2, and d3v/3xdt2. In the context of the separation of variables, these conditions lead to corresponding con­straints on some or all of the following at the ends: X, X’, X", and X"’. The resulting four boundary conditions on X and its derivatives are necessary and sufficient for determination of the four constants Ci, Di, or Ei (i = 1, 2, 3, and 4) to within a multiplicative constant.

As with torsion, the nature of the boundary conditions at an end stems from how that end is restrained. When an end cross section is unrestrained, the tractions on it are identically zero. Again, the most stringent condition is a perfect clamp, which for bending allows neither translation nor rotation of an end cross section. Like the clamped-end condition in torsion, the clamped end in bending is a common idealization, although nearly impossible to achieve in practice.

For the bending problem, a wide variety of cases that only partially restrain an end cross section is possible. The cases typically involve elastic and/or inertial reactions. A boundary condition that is idealized in terms of both translational and rotational springs may be used to more realistically account for support flexibility. Appropriate values for both translational and rotational flexibility of the support can be estimated from static tests. Finally, we can use rigid bodies and springs in combination to model attached hardware such as fuel tanks, engines, armaments, and laboratory fixtures.

Figure 3.25. Schematic of pinned-end condition

In this section, we consider the four “primitive” boundary conditions; four de­rived boundary conditions involving individual elastic and inertial restraints; and two examples of derived boundary conditions that involve combinations of v and its partial derivatives that can be imposed at the ends of the beam for determination of the four arbitrary constants of the general solution for X.

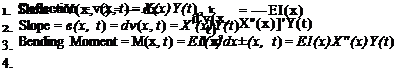A boundary condition can be written as a linear relationship involving one or more of the following: the beam deflection, its first three spatial partial derivatives, and its first two temporal partial derivatives. Although it is not a mathematical requirement, the particular combination of conditions to be specified at a beam end should represent a physically realizable constraint. The various spatial partial derivatives of the beam deflection can be associated with particular beam states at any arbitrary point along the beam. There are four such states of practical interest:

When relating these beam states, the positive convention for deflection and slope is the same at both ends of the beam. In contrast, the sign conventions on shear and bending moment differ at opposite beam ends, as illustrated by the free-body differential beam element used to obtain the equation of motion (see Fig. 2.6).

The most common conditions that can occur at the beam ends involve vanish­ing pairs of individual states. Typical of such conditions are the following classical configurations (specialized for spanwise uniformity):

• Clamped or built-in end, which implies zero deflection and slope, is illustrated in Fig. 3.10 and has v(£, t) = dv(£, t) = 0 so that X(£) = X'(£) = 0.

• Free end, which corresponds to zero bending moment and shear, is illustrated in Fig. 3.11 and has M(£, t) = V(£, t) = 0 so that X"(£) = X’"(£) = 0.

• Simply supported, hinged, or pinned end, which indicates zero deflection and bending moment, is denoted by the triangular symbol in Fig. 3.25 and has v(£, t) = M(£, t) = 0 so that X(£) = X"(£) = 0.

• Sliding end, which corresponds to zero shear and slope, is illustrated in Fig. 3.26 and has dv(£, t) = V(£, t) = 0 so that X'(£) = X’"(£) = 0.

All of these conditions can occur in the same form at x = 0.

Figure 3.26. Schematic of sliding-end condition

In addition to these zero-state conditions, we derive boundary conditions corre­sponding to linear-constraint reactions associated with elastic and inertial elements. The simplest of these are of the following four basic types:

• translational elastic constraint

• rotational elastic constraint

• translational inertia constraint

• rotational inertia constraint

Two additional examples are presented that are more involved because they entail combinations of these four types.

Translational Elastic Constraint. Consider a beam undergoing bending with a trans­lational spring with elastic constant к attached to the x = 0 end of a beam, as shown in Fig. 3.27. Assuming that this end of the beam is deflected by the amount v(0, t), then the spring tries to pull the end of the beam back to its original position by exerting a downward force at the end, the magnitude of which is equal to kv(0, t). Because the transverse-shear force at the left end (on the negative x face) is positive down, the boundary condition becomes

V(0, t) = kv(0, t) (3.207)

Using the definition of the shear force, we obtain

– Tx(E S)(at) = kv(0-‘) (3208)

To be useful for separation of variables, we must make the substitution v(x, t) = X(x)Y(t), yielding

[E7(0) X(0)7 = – kX(0) (3.209)

kv(0,t)

(b) beam with spring force

Figure 3.27. Example beam undergoing bending with a spring at the x = 0 end

x=0 x=l

к——————— £——————— *

which further simplifies for a spanwise uniform beam to

E7X" (0) = – kX(0) (3.210)

If the spring were at x = I instead, the direction of the spring force at x = I would be the same (i. e., downward), but the shear force is positive upward because this is the positive x face. Thus

V(l, t) = – kv(l, t) (3.211)

and

[E7(l) X(l)"Y = kX(t) (3.212)

which further simplifies for a spanwise uniform beam to

~E7X’"(l) = kX(l) (3.213)

These conditions must be augmented by one additional condition at each end because two are required. For example, consider a beam with translational springs at both ends, as shown in Fig. 3.28. At each end, the other conditions for this case would be that the bending moment is equal to zero.

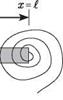
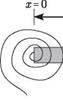
Rotational Elastic Constraint. Consider now a beam with a rotational spring at the right end, as depicted in Fig. 3.29. For a rotation of the end cross-sectional plane of dv/dx at x = l, which is positive in the counterclockwise direction, the spring exerts a moment in the opposite direction (i. e., clockwise). Because the bending moment at the right end of the beam is positive in the counterclockwise direction, the boundary condition then becomes

dv

M(l, t) = – k (l, t) (3.214)

к к

.WYvWW’ W\\\

Figure 3.30. Schematic of beam with rotational springs at both ends

Using the definition of bending moment, we find

д 2v dv

EI ) = – k~*{u) (3-215)

The boundary condition on X then becomes

ElX”(l) = – kX'(l) (3.216)

As with the shear force, the sign convention on bending moment differs at the opposite end. Here, at the left end, the spring still exerts a clockwise moment; however, the bending moment is also positive in the clockwise direction. Thus, we may write

dv

M(0, t) = k — (0, t)

д X

ш S(0-t)=кд (0-t)

for the condition on v(x, t) and its partial derivatives and

ElX"(0) = kX’ (0)

for that on X(x) and its derivatives. As before, one more condition is required at each end. Consider, for example, a beam with rotational springs at both ends, shown in Fig. 3.30. Here, it is necessary to set the shear forces at both ends equal to zero.

Translational and Rotational Inertia Constraints. The translational inertia con­straint stems from the inertial reaction force associated with the translational motion of either a rigid body or a particle attached to an end of a beam. Similarly, the ro­tational inertia constraint results from the inertial reaction moment associated with rotational motion of a rigid body attached to an end of a beam.

Consider the beam shown in Fig. 3.31, to which is attached a rigid body of mass mc and mass moment of inertia about the mass center C equal to IC. The point C is located on the x axis at x = 0, and the beam is assumed to be undergoing bending deformation. The set of all contact forces exerted on the body by the beam can be replaced by a single force applied at the point C, and the moment of those contact forces about C. The resultant of all of those contact forces is simply the shear force U(0, t); their moment about C is the bending moment M(0, t).

(a) Beam with rigid body
attached at x=0

Figure 3.31. Schematic of rigid body (a) attached to end of a beam, and (b) detached showing interactions

Therefore, Euler’s first and second laws take on the form

d 2 v

V(0, t) = mc d72 (0, t)

d 2v

M(0’t) = * ЩЕ-(0-t)

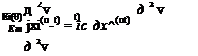which in terms of v and its partial derivatives become, respectively,

To determine the boundary conditions on X, we first substitute v(x, t) = X(x)Y(t) as before, yielding

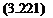-[ EI(0) X //(0)]/Y(t) = mcX(0)Y(t) EI(0) X "(0)Y(t) = IcX'(0)Y(t)

Recalling from the second of Eqs. (3.197) that Y + m2Y = 0, these relationships simplify to

-[ EI(0) X//(0)]/ = – mc «2 X(0) EI(0) X "(0) = – ic о? X ‘(0) which, for a spanwise uniform beam, may be simplified to

mX //7(0) = mc a4 X(0) mX "(0) = – ic a4 X ‘(0)

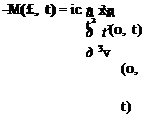Eqs. (3.223) apply when a rigid body is attached to a free end. For a particle, we may simply set ic = 0. Finally, at the opposite end of the beam, we need only change the signs of the stress resultants, so that

(a) beam with positive stress resultants at x=l

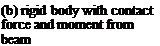
Figure 3.32. Example with rigid body attached to the right end of beam undergoing bending

from which we may express boundary conditions on Xfor a spanwise uniform beam, given by

mX"'(l) = — mc a4 X(£) mX"(f) = IC a4 X ‘(€)

It is appropriate to note that the use of the second of Eqs. (3.225) allows us to express Eqs. (3.197) as

V(f, t) = mca/v(0, t)

9 (3.:

M(f, t) = Ic«2 ^ (0, t)

д X

subject to the restriction that these conditions hold true only for free vibration.

Other Boundary Configurations. We now turn our attention to two more examples, which are only slightly more involved. First, we consider a beam with an attached rigid body of mass mc and moment inertia about C given by IC. The body has a mass center that is offset from the point of attachment (at x = f) by a distance e, as shown in Fig. 3.32. (This is unlike the previous case in which the body mass center C is located at x = f and thus has e = 0; see Fig. 3.31.) The body mass center C is assumed to be on the x axis so that transverse vibrations do not excite torsional vibrations and vice versa. The sum of all forces acting on the body is

(LF)y s-V(f-‘)

Euler’s first law says that this should be equated to the mass times the acceleration of C. The acceleration of C in the y direction can be written as

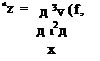where the body’s angular acceleration about the z axis (normal to the plane of the paper) is

Thus, Euler’s first law for the body is

Figure 3.33. Example with mechanism attached to the left end of beam undergoing bending

The sum of the moments about C in the z direction

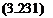
(l]Mc)z = – M(£, t) + eV(l, t)

d 3 v

d 12д X Eqs. (3.230) and (3.232) can be combined to solve for V(l, t) and M(l, t), yielding d3v „ d2v

d 3v

Euler’s second law says that this should be equated to the moment of inertia about C times the angular acceleration about the z axis, so that

The last example involves a mechanism attached to the left end of a beam with a pinned connection to ground, as shown in Fig. 3.33. The massless rigid rod is of length h and the particle has mass mc; this combination should be considered a rigid body with mass mc and moment of inertia about the pivot mch2. The massless rod is embedded in the left end of the beam and rotates with it. A positive rotation of the x = 0 cross-sectional plane about the normal to the page (i. e., the z axis) is counterclockwise and has the value

dv

№ t) = T-(0, t) (3.235)

д X

This rotation results in the downward motion of the particle by the distance hp (0, t) and leads to the upward force exerted by the spring, khp(0, t). Thus, this body has a free-body diagram, as shown in Fig. 3.34. A rotation of the rigid body is positive in the counterclockwise direction. Denoting the pivot as O, we find that the sum of moments on the mechanism is

(EMo)z = M(0, t) – kh2dv(0, t)

beam

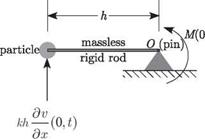Figure 3.34. Free-body diagram for example with mechanism attached to the left end of beam undergoing bending

Here, Euler’s second law is applied about the pivot to avoid dealing with reaction forces at O. This requires us to equate the sum of the moments about O to the moment of inertia about O times the angular acceleration; viz.

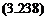dv d 3 v

M(°’ )- uh ix (°’ )="kl’2 wxx (°’ )

or

EI S<°’’ )- k’2 ё (0t ) = ”""2 ШХ (0t )

The corresponding boundary condition on X at x = ° is found to be

As always with bending problems, one other boundary condition applies at x = ° for the configuration shown in Fig. 3.33—namely, v(°, t) = X(°) = °.