Boundary-Layer Equations

The boundary layer can be considered as the phenomenological model of attached viscous flow. We derive in the following the boundary-layer equa­tions for steady, compressible, three-dimensional flow past a flat surface. We assume laminar flow, but note that the resulting equations also hold for tur­bulent flows, if we treat them as Reynolds – or Favre-averaged flows [1, 6].

The derivation is made in Cartesian coordinates. We keep the notation introduced in Fig. 4.1 with x and z (z not indicated there) being the coor­dinates tangential to the body surface, and y the coordinate normal to it.

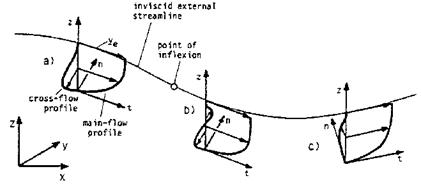
Fig. 7.2. Streamline curvature and cross-flow profiles of a three-dimensional bound­ary layer (schematically) [3]: a) negative cross-flow profile, b) s-shaped cross-flow profile, c) positive cross-flow profile. The coordinates t and n are tangential to the body surface, г is normal to the body surface.

Accordingly u and w are the tangential velocity components, and v is the component normal to the body surface.[86]

We try to keep the derivation as simple as possible in order to concentrate on the basic physical problems. (That is also the reason why we employ Cartesian coordinates.) Therefore, we do not include the description of the typical phenomena connected with hypersonic attached flow like the extra formulations for high-temperature real-gas effects, surface-radiation cooling, and slip-flow effects. Their introduction into the resulting system of equations is straight forward.

The boundary-layer equations are derived from the Navier-Stokes equa­tions, together with the continuity equation and the energy equation, Sub­Section 4.3. They cannot be derived from first principles [1]. One has to intro­duce the observation—the boundary-layer assumption, originally conceived by L. Prandtl [7]—that the extension of the boundary layer in direction normal to the body surface (coordinate y and the involved boundary-layer thicknesses) is very small, like also the velocity component v in the boundary layer normal to the body surface. Actually the observation is that the differ­ent boundary-layer thicknesses and v in y-direction are inversely proportional to the square root of the Reynolds number.

We take care of this observation by introducing the so-called boundary – layer stretching, which brings y and v, non-dimensionalized with reference data Lref and vref, respectively, to O(1):

Reref = Preft’re/Lre/ . (7.3)

ftref

The prime above denotes variables, which were non-dimensionalized and stretched, however, we use it in the following also for variables, which are only non-dimensionalized.

All other variables are simply made dimensionless with appropriate refer­ence data, and assumed then to be O(1): velocity components u and w with vref, lengths x and z with Lref, temperature T with Tref, density p with pref, pressure p with prefv? ff, the transport coefficients /л and к with /i, ref and kref, respectively, and finally the specific heat at constant pressure cp with cPref.4 Each resulting dimensionless variable is marked by a prime, for instance

u’ = —. (7.4)

vref

We introduce boundary-layer stretching and non-dimensionalization first into the continuity equation, eq. (4.83). We do this for illustration in full detail. In three dimensions and without the partial time derivative, Section 4.1, we replace и with u’vref, eq. (7.4), v with v’vrefjjReref, eq. (7.2), etc, and find

df/prefu’vref ^ dp’prefv’yref/-sjReref ^ dp’pref w’vref _ 0 ^ ^

Ox Lref dy’Lref/ уReref k)z Lrej

Because all reference parameters, and also Reref are constants, we find immediately the stretched and dimensionless continuity equation which has the same form—this does not hold for the other equations—as the original equation:

4 In classical boundary-layer theory the pressure is made dimensionless with Pref v2ref, which has the advantage that the equations describe in this form both compressible and incompressible flows. For general hypersonic viscous flows, how­ever, we choose pref to make the pressure dimensionless, Sub-Section 7.1.7.

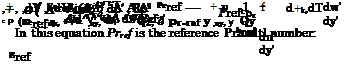Again we introduce non-dimensional and stretched variables, as we did above. We also write explicitly all terms of O(1), and bundle together all terms, which are of smaller order of magnitude, now except for two of the heat-conduction terms:and Eref the reference Eckert number:

Eref = (jref — l)Mref ■ (7.22)

(Both were introduced in Sub-Section 4.3.2.)

We have retained on purpose in this equation two terms, which are nom­inally of lower order of magnitude. They are the gradients of the heat – conduction terms in x and z direction, which are of O(l/Reref). The reason is that we in general consider radiation-cooled surfaces, where we have to take into account possible strong gradients of Tw in both x and z direction. They appear there on the one hand, because the thermal state of the surface changes strongly in the down-stream direction, usually the main-axis direc­tion of a flight vehicle, Chapter 3. On the other hand, strong changes are present in both x and z direction, if laminar-turbulent transition occurs, see, e. g., Sub-Section 7.3.

The question now is, under what conditions can we drop the two terms, regarding the changes of the wall temperature. To answer it, we follow an argumentation given by Chapman and Rubesin [10]. We consider first (in two dimensions) the gradient of the heat-conduction term in direction normal to the surface in dimensional and non-stretched form, eq. (7.19), and introduce finite differences, as we did in Sub-Section 3.2.1:

with 5T being the thickness of the thermal boundary layer.

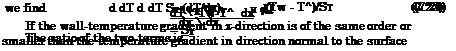
The gradient of the heat-conduction term in x-direction is written, as­suming that (dT/dx)w is representative for it

The result is: provided, that eq. (7.26) holds, the gradient term of heat conduction in ж-direction can be neglected, because St/L ос 1/(/Pr/Re) ^ 1 in general means

d dT d dT

« Ж,(к 17’■

In [10] it is assumed, that the recovery temperature is representative for the wall temperature

Tw=Tr= TU1 + г^-ІАф. (7.29)

Introducing this into eq. (7.26), together with St ~ S « cL/^/Reref for laminar flow, we obtain

With r = y/Pr = a/0.72, Y = 1.4, c = 6 we arrive finally, after having in­troduced non-dimensional variables, at the Chapman-Rubesin criterion [10]. It says that the term eq. (7.24) can be neglected, if

dT’

— |ш ^ <U>3.l/:( x H,,. (7.31)

This means, that, for instance, for M^ = 1 and Reref = 106, the max­imum permissible temperature gradient would be equivalent to a thirty-fold increase of T/T^ along a surface of length Lref. From this it can be con­cluded, that in general for high Mach-number and Reynolds-number flows the Chapman-Rubesin criterion is fulfilled, as long as the surface-temperature distribution is “reasonably smooth and continuous”. The situation can be different for low Mach numbers and Reynolds numbers.

With radiation-cooled surfaces, as we noted above, we do not necessarily have reasonably smooth and continuous surface-temperature distributions in both x and z direction. Moreover, the basic relation eq. (7.23) needs to be adapted, because it does not describe the situation at a radiation-cooled surface. For that situation we introduce a slightly different formulation for both directions:

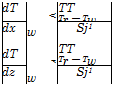(7.32)

(7.32) because, at least for laminar flow, Tr — Tw is the characteristic tempera­ture difference, see Sub-Section 3.2.2. We also introduce the absolute values dT/dxw and dT/dzw, because the gradients will be negative downstream
of the forward stagnation point, Sub-Section 3.2.1, but may be positive or negative in laminar-turbulent transition regimes, Sub-Section 7.3, and in hot­spot and cold-spot situations, Sub-Section 3.2.4.

The modified Chapman-Rubesin criterion is then: if eqs. (7.32) and (7.33) hold, the gradient term of heat conduction in both x and ^-direction can be neglected, because again St/L ос 1/(/Pr/Re)

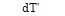
__L___ d_

Reref dx’

1 d ‘ Reref dz

We refrain to propose detailed criteria, like the original Chapman-Rubesin criterion, eq. (7.31). This could be done for the region downstream of the forward stagnation point, but not in the other regimes. In practice the results of an exploration solution should show, if and where the modified Chapman- Rubesin criterion is violated or not and whether the two tangential heat conduction terms must be kept or not.[87]

Provided that the modified Chapman-Rubesin criterion is fulfilled, we arrive at the classical boundary-layer equations by neglecting all terms of O(1/Reref) and O(1/Re2ref) in eqs. (7.6), (7.16) to (7.18), and (7.20). We write the variables without prime, understanding that the equations can be read in either way, non-dimensional, stretched or non-stretched, and dimen­sional and non-stretched, then without the similarity parameters Prref and

Eref :

	dpu dpv dx dy	g о c§" ^ +	= 0,		(7.36)
du	du	du	dp	d	f du	(7.37)
fmd~x	+ ,n% +	PWTz	dx	+ % 1	V%) ’
		0 = –	dp dy’			(7.38)
dw	dw	dw	dp	d	f dw	(7.39)
PU^	+ ""% +	pwlb	dz	+ dy	Ы) ’

du 2 / dw 2 1 dy) +dy) j

These equations are the ordinary boundary-layer equations which describe attached viscous flow fields on hypersonic flight vehicles. If thick boundary layers are present and/or entropy-layer swallowing occurs, they must be em­ployed in second-order formulation, see below. For very large reference Mach numbers Mref the equations become fundamentally changed, see Sub-Section 7.1.7.[88]

With the above equations we can determine the unknowns u, v, w, and T. The unknowns density p, viscosity p, thermal conductivity k, and specific heat at constant pressure cp are to be found with the equation of state p = pRT, and the respective relations given in Chapters 4 and 5. If the boundary – layer flow is turbulent, the apparent transport properties must be introduced, [1] and Section 8.5. If high-temperature real-gas effects are present in the flow field under consideration, the respective formulations and laws must be incorporated.

Since dp/dy is zero, the pressure field of the external inviscid flow field, represented by dp/dx and dp/dz, is imposed on the boundary layer. This means, that in the boundary layer dp/dx and dp/dz are constant in y – direction. This holds for first-order boundary layers. If second-order effects are present, dp/dx and dp/dz in the boundary layer are implicitly corrected via dp/dy = 0 by centrifugal terms, see below.

The equations are first-order boundary-layer equations, based on Carte­sian coordinates. In general locally monoclinic surface-oriented coordinates, factors and additional terms are added, which bring in the metric proper­ties of the coordinate system [1]. It should be noted, that the equations for the general coordinates are formulated such that also the velocity com­ponents are transformed. This is in contrast to modern Euler and Navier – Stokes/RANS methods formulated for general coordinates. There only the geometry is transformed, Section A, and not the velocity components.

If locally the boundary-layer thickness is not small compared to the small­est radius of curvature of the surface, the pressure gradient in the boundary layer in direction normal to the surface, dp/dy, is no longer small of higher order, and hence no longer can be neglected.[89] This is a situation found typically in hypersonic flows, where also entropy-layer swallowing can oc­
cur, Sub-Section 6.4.2. This situation is taken into account by second-order boundary-layer equations, which basically have the same form as the first – order equations [1, 12]. Information about the curvature properties of the surface is added. The y-momentum equation does not degenerate into dp/dy = 0. dp/dy is finite because centrifugal forces have to be taken into account. At the outer edge of the boundary layer the boundary conditions are deter­mined by values from within the inviscid flow field, not from the surface as in first-order theory, see the discussion in Sub-Section 6.4.2. Also the first derivatives of the tangential velocity components, of temperature, density and pressure are continuous [12], which is not the case in first-order theory, see, e. g., Fig. 6.23.