Direct Curve Fitting

Curve fitting the airfoil characteristics using higher-order polynomials is another possible way of representing the nonlinear airfoil characteristics in the high AoA regime. Various strategies are possible, but caution should be used. For example, the lift

may be represented using

(7.102)

Generally, as low an order of polynomial as possible would be used. Typically, N = 3 gives a reasonable approximation. Alternatively, a ratio of polynomials of the form

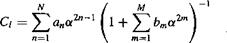
(7.103)

will often prove acceptable. In each case, the coefficients in the series are obtained in a least-squares sense.

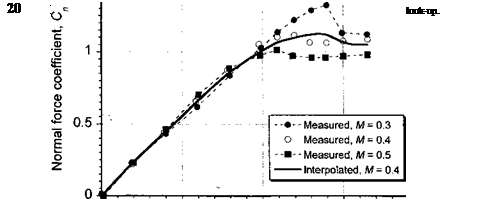
As shown in Fig. 7.49, comparisons of direct curve fitting techniques with test data are reasonably adequate but tend to underpredict the magnitude of the airloads near maximum lift and also change the nature of the stall characteristic. This is typical whenever the airloads change rapidly with respect to AoA. However, single polynomial representations generally do not work well over an extended range of AoA.

Alternatively, the representation of the airfoil characteristics can be broken into smaller ranges of AoA. For example, one curve can be used below stall, and another curve(s) in the post stall regime, while requiring that the curves be piecewise continuous. This method has some difficulties, however, especially when interpolating the curve fit coefficients and break points between Mach numbers. Also, the conditional branching in the computer program consumes more time, which may not be acceptable in some applications, especially real-time flight simulation work where computational speed is paramount.