Effects of Reynolds Number
At low Mach numbers, variations in Reynolds number will affect both the type of stall and the maximum lift coefficient. A fundamental study of the relationships was first made by Jacobs & Sherman (1937). Increasing the Reynolds number increases the inertial effects in the flow, which will dominate over the viscous effects and, all other factors being
|
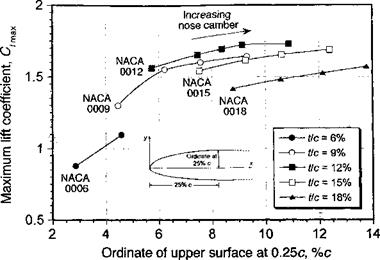
Figure 7.34 Results showing effect of nose camber on C/max. Data source: Jacobs et al. (1937). |
equal, will thin the boundary layer and delay the onset of flow separation to higher values of AoA and lift coefficient. Figure 7.35 shows the effects of increasing Reynolds number for the NACA 63- and 64-series airfoils. The main trend is an increase in C;max, but at a very small rate after a certain value of Re is reached. The main difficulty in assessing the effects of Reynolds number is the interdependent effects of Mach number. The Mach number, M^, may be written in terms of the Reynolds number, Re, as
A/oo = (—)—, (7.87)
paj c
|
Figure 7.35 Effect of Reynolds number on the maximum lift coefficient of the NACA 63-series and 64-series airfoils. Data source: Racisz (1952). |
|
Free-stream Mach number, M Figure 7.36 Results of independent Reynolds number and Mach number variations on the CW of a NACA 64-210 airfoil. Data source: Racisz (1952). |
where c is the airfoil chord. Unless special (pressurized) wind tunnels are used where the Reynolds number can be varied completely independently of Mach number, Eq. 7.87 shows that a change in free-stream Mach number will always be accompanied by a change in Reynolds number and vice versa.
up to Mach numbers of about 0.4, the effects of varying Reynolds number on the maximum lift and stall characteristics can be significant. For example, results showing the independent Mach number and Reynolds number variation on the maximum lift of a NACA 64-210 airfoil section are given in Fig. 7.36. These data show that the Reynolds number has a strong influence on the maximum lift capability at a given Mach number, with larger Reynolds number leading to higher values of C/max for a given Mach number. At higher free – stream Mach numbers the effects of Reynolds number are secondary compared to the effects of compressibility, as confirmed by the fact that curves for each Reynolds number show a converging trend. These effects of interdependent Reynolds number and Mach number should be borne in mind when analyzing results from subscale rotor tests, where the blade Reynolds numbers may be one-quarter or less of the full-scale rotor values.
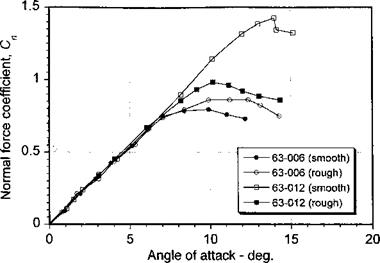
In addition to the effects of Reynolds number and airfoil shape, any roughness on the leading edge of the airfoil may also affect the stall type. Surface roughness causes premature transition from a laminar to a turbulent boundary layer, thereby increasing the effective Reynolds number. Generally, prematurely tripping the boundary layer will always make the airfoil exhibit a trailing edge (gradual) stall, whereby the point of turbulent separation moves forward on the chord with increasing AoA. In wind tunnel experiments, standard roughness is applied to the airfoils in the form of carborundum grains or other standardized approaches – see, for example, Loftin (1945) and Abbott & von Doenhoff (1949). In the case of an airfoil that initially exhibits thin-airfoil stall, leading edge roughness will eliminate the laminar separation bubble and will always give the airfoil a gradual turbulent trailing edge stall characteristic (see Fig. 7.37). As shown by the NACA 63-006 airfoil, this is usually accompanied by a mild increase in C/max. However, the application of standard roughness to an airfoil that initially exhibits leading edge stall will cause the boundary layer to be more susceptible to turbulent boundary layer separation at a lower AoA. Therefore, as shown by
|
Figure 7.37 Effect of leading edge roughness on the low-speed lift and stall characteristics of the 63-006 and 63-012 airfoils: Data source: Abbott & von Doenhoff (1949). |
the 63-012 airfoil, this results in a gradual trailing edge stall characteristic and a significant loss of maximum lift capability.